Complete Light Reflection & Refraction Notes
Master all concepts with ray diagrams, 25+ examples, and NCERT-based explanations for Class 10 CBSE exams.
Table of Contents
1 Reflection of Light
Laws of Reflection
When light hits a surface (like a mirror), it follows two fundamental laws:
- First Law: Incident ray, reflected ray, and normal all lie in the same plane.
- Second Law: Angle of incidence (∠i) = Angle of reflection (∠r).
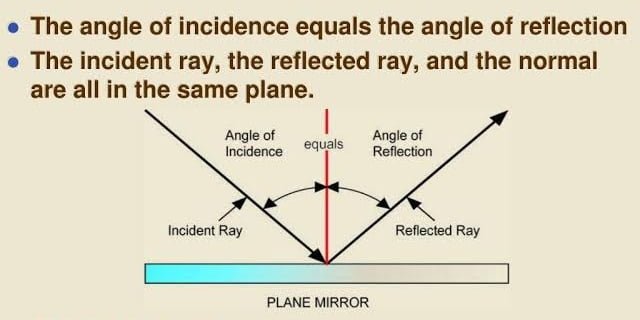
Fig 1.1: Reflection at plane surface
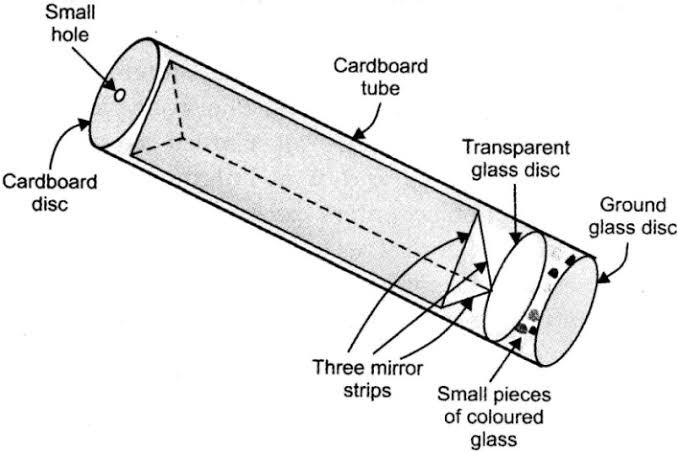
Real-World Example: Kaleidoscope
A kaleidoscope uses multiple mirrors (usually 3) arranged at 60° angles to create symmetrical patterns through repeated reflections.
How it works:
- Light enters through colored objects at the end
- Undergoes multiple reflections between mirrors
- Creates beautiful symmetrical patterns
2 Spherical Mirrors
Concave Mirror
Properties:
- Reflecting surface curves inwards
- Focal length (f) is negative
- Converges parallel light rays to focus
Uses:
- Shaving mirrors: Produces magnified erect image when object is between pole and focus
- Headlights: Reflectors use parabolic concave mirrors to produce parallel beam
- Telescopes: Large concave mirrors collect light from celestial objects
Convex Mirror
Properties:
- Reflecting surface curves outwards
- Focal length (f) is positive
- Diverges parallel light rays (appear to come from focus)
Uses:
- Rear-view mirrors: Provides wider field of view (though images are diminished)
- Security mirrors: Used in stores to monitor large areas
- Road safety: Installed at blind turns to see incoming traffic
Important Terms
| Term | Symbol | Definition |
|---|---|---|
| Pole | P | Center point of mirror surface |
| Radius of Curvature | R | Radius of the sphere from which mirror is cut (R = 2f) |
| Principal Focus | F | Point where parallel rays converge (concave) or appear to diverge (convex) |
3 Ray Diagrams for Spherical Mirrors
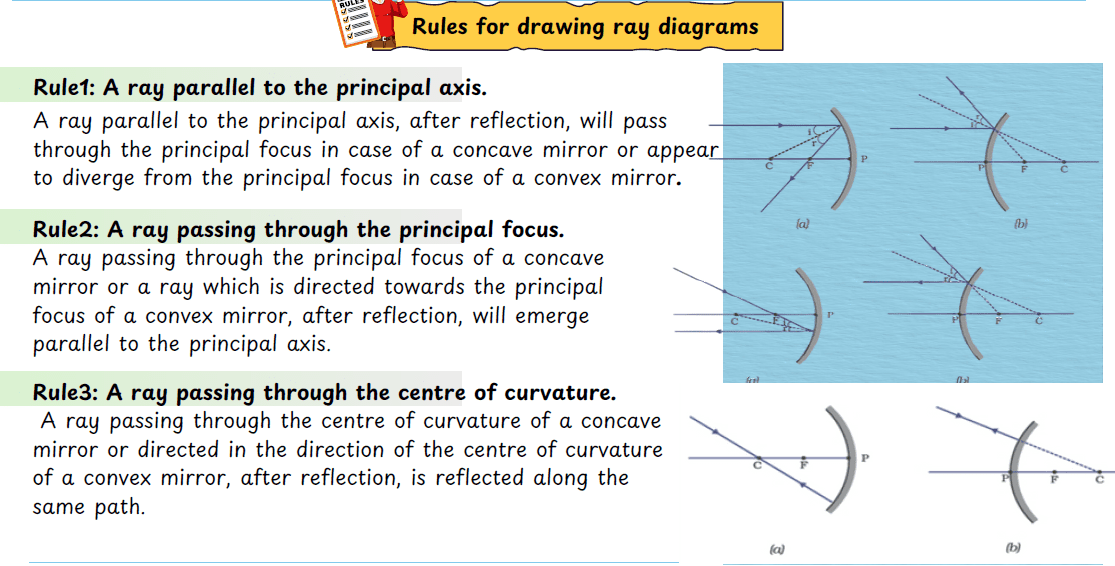
Rules for Drawing Ray Diagrams
Rule 1: Ray parallel to principal axis passes through focus after reflection (concave) or appears to diverge from focus (convex).
Rule 2: Ray passing through focus becomes parallel to principal axis after reflection (concave). For convex, ray directed toward focus becomes parallel.
Rule 3: Ray passing through center of curvature (C) reflects back along same path.
Concave Mirror Image Formation
Case 1: Object beyond C
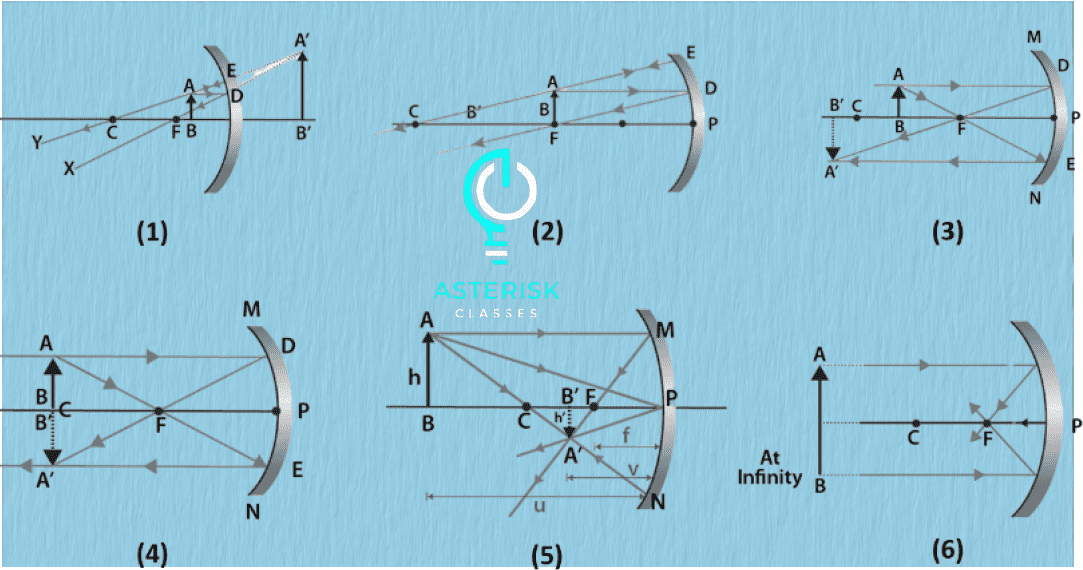
Real, inverted, diminished (between F and C)
Case 2: Object at C

Real, inverted, same size (at C)
Convex Mirror Image Formation
All object positions
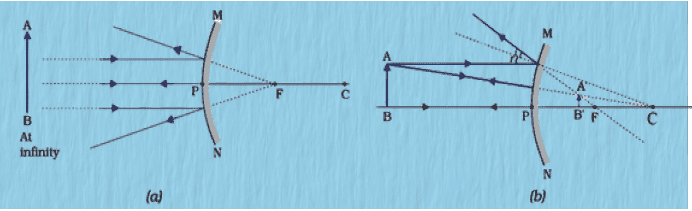
Always virtual, erect, diminished (between P and F)
4 Mirror Formula & Magnification
Mirror Formula Derivation
The mirror formula relates object distance (u), image distance (v), and focal length (f):
1/f = 1/v + 1/u
Sign Convention:
- Object distance (u): Always negative for real objects
- Image distance (v): Negative for real images, Positive for virtual images
- Focal length (f): Negative for concave, Positive for convex
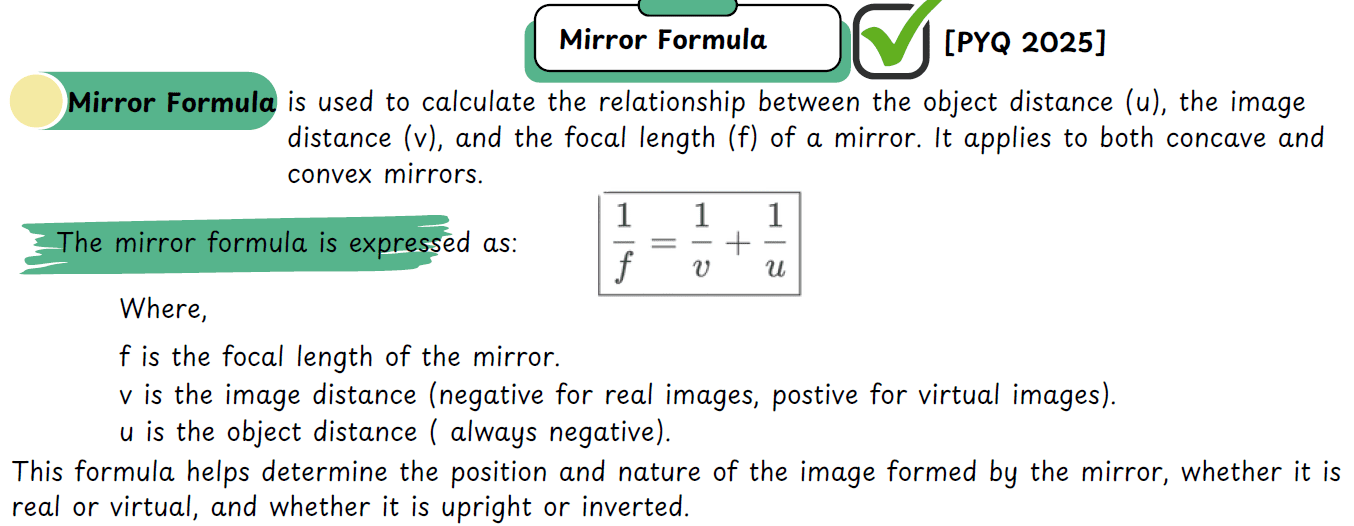
Numerical Example
Problem: An object is placed 20 cm from a concave mirror of focal length 15 cm. Find image position and nature.
Given: u = -20 cm, f = -15 cm (concave mirror)
Using mirror formula: 1/f = 1/v + 1/u
⇒ 1/(-15) = 1/v + 1/(-20)
⇒ -1/15 + 1/20 = 1/v
⇒ (-4 + 3)/60 = 1/v ⇒ v = -60 cm
Interpretation: Image forms 60 cm in front of mirror (real, inverted), magnification m = -v/u = -3 (enlarged).
5 Refraction of Light
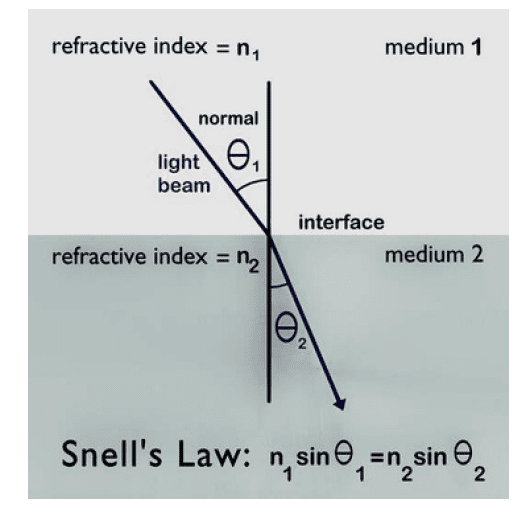
Laws of Refraction (Snell’s Law)
When light passes from one medium to another (e.g., air to glass):
- First Law: Incident ray, refracted ray, and normal lie in same plane.
- Second Law: n₁ sin i = n₂ sin r (Snell’s Law), where:
- n₁, n₂ = refractive indices
- i = angle of incidence
- r = angle of refraction
Refractive Index
Refractive index (n) measures how much a medium bends light:
n = speed of light in vacuum / speed of light in medium
Examples:
- Air: n ≈ 1.0003
- Water: n = 1.33
- Glass: n ≈ 1.5-1.7
- Diamond: n = 2.42
Real Example: Apparent Depth
When viewing a pool, objects appear shallower due to refraction:
Apparent depth = Real depth / n
If a pool is 2m deep (n=1.33), it appears to be 1.5m deep.

6 Lenses
Convex Lens (Converging)
Properties:
- Thicker at center than edges
- Focal length (f) is positive
- Forms real inverted or virtual erect images
Uses:
- Magnifying glass: When object is between F and lens
- Camera lenses: Focus light onto film/sensor
- Correcting hypermetropia: Helps focus light onto retina
Concave Lens (Diverging)
Properties:
- Thinner at center than edges
- Focal length (f) is negative
- Always forms virtual, erect, diminished images
Uses:
- Correcting myopia: Diverges light before it enters eye
- Peepholes: Provides wide-angle view
- Laser beam expanders: Used in optical instruments
Lens Formula & Power
The lens formula is similar to mirror formula but with different sign convention:
1/f = 1/v – 1/u
Power of Lens:
P = 1/f (where f is in meters)
- Unit: Diopter (D)
- Convex lens: Positive power
- Concave lens: Negative power

Numerical: Spectacle Power
Problem: A concave lens has focal length 50 cm. What is its power?
Given: f = -50 cm = -0.5 m (concave lens)
Power P = 1/f = 1/(-0.5) = -2 D
Interpretation: This is a diverging lens used to correct myopia.
Key Summary
Reflection:
- ∠i = ∠r (plane surfaces)
- Concave mirrors: Real/inverted or virtual/erect images
- Convex mirrors: Always virtual/diminished
Refraction:
- n₁ sin i = n₂ sin r (Snell’s Law)
- Convex lenses converge light, concave diverge
- Power of lens (P) = 1/f (in meters)
Exam Checklist
- Memorize sign conventions for mirrors and lenses
- Practice drawing ray diagrams for all cases
- Learn refractive indices of common materials
- Understand applications (spectacles, microscopes, etc.)
Complete Chapter Notes
Access the detailed notes I’ve prepared covering all NCERT concepts, reactions, and important questions: