Exercise 10.1 Solutions
Circles
1. How many tangents can a circle have?
A circle is a collection of infinitely many points in a plane. A tangent can be drawn to the circle at each of these points.
Answer: A circle can have infinitely many tangents.
2. Fill in the blanks:
(i) A tangent to a circle intersects it in one point(s).
By definition, a tangent touches a circle at exactly one point.
(ii) A line intersecting a circle in two points is called a secant.
This is the definition of a secant of a circle.
(iii) A circle can have two parallel tangents at the most.
These two parallel tangents can be drawn at the two ends of any diameter of the circle.
(iv) The common point of a tangent to a circle and the circle is called point of contact.
This is the specific name for the point where the tangent touches the circle.
3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Length PQ is:
(A) 12 cm (B) 13 cm (C) 8.5 cm (D) √119 cm.
Step 1: Understand the geometry.
The radius from the center to the point of tangency (OP) is perpendicular to the tangent (PQ). Therefore, ΔOPQ is a right-angled triangle with the right angle at P.
Step 2: Identify the given values.
Radius, OP = 5 cm.
Distance from center to Q, OQ (Hypotenuse) = 12 cm.
We need to find the length of the tangent, PQ.
Step 3: Apply the Pythagorean theorem.
In right ΔOPQ, OP² + PQ² = OQ².
5² + PQ² = 12²
25 + PQ² = 144
PQ² = 144 – 25 = 119
PQ = √119 cm.
Answer: (D) √119 cm.
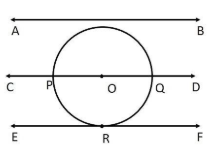
4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Construction Steps:
1. Draw any circle with center O and a given line l outside it.
2. Draw a line m perpendicular to the line l that passes through the center O of the circle. Let this line intersect the circle at points A and B.
3. Draw a line p through point A, parallel to the given line l. This line p is the required tangent to the circle.
4. Draw a line q parallel to the given line l that intersects the circle at two distinct points (for example, a line between O and A). This line q is the required secant to the circle.
 >
>

