Exercise 8.1 Solutions (Class 9)
Quadrilaterals
1. If the diagonals of a parallelogram are equal, then show that it is a rectangle.
Given: A parallelogram ABCD where diagonal AC = diagonal BD.
To Prove: ABCD is a rectangle.
Proof:
Consider ΔABC and ΔDCB.
• AB = DC (Opposite sides of a parallelogram are equal)
• BC = CB (Common side)
• AC = DB (Given)
By SSS congruence, ΔABC ≅ ΔDCB.
Therefore, ∠ABC = ∠DCB (by CPCT).
Also, since AB || DC and BC is a transversal, the sum of consecutive interior angles is 180°.
∠ABC + ∠DCB = 180°.
Since ∠ABC = ∠DCB, we have 2∠ABC = 180° => ∠ABC = 90°.
A parallelogram with one right angle is a rectangle. (Proved)
2. Show that the diagonals of a square are equal and bisect each other at right angles.
Given: A square ABCD with diagonals AC and BD intersecting at O.
To Prove: (i) AC = BD, (ii) AO=OC, BO=OD, and (iii) ∠AOB = 90°.
Proof:
(i) Diagonals are equal: In ΔABC and ΔDCB, AB=DC, BC=CB, ∠ABC=∠DCB=90°. By SAS, ΔABC ≅ ΔDCB. So, AC = BD (CPCT).
(ii) Diagonals bisect each other: In ΔAOB and ΔCOD, AB=CD, ∠OAB=∠OCD (alt. int. angles), ∠OBA=∠ODC (alt. int. angles). By ASA, ΔAOB ≅ ΔCOD. So, AO=OC and BO=OD (CPCT).
(iii) Diagonals bisect at right angles: In ΔAOB and ΔCOB, AO=OC (proved), OB=OB (common), AB=BC (sides of a square). By SSS, ΔAOB ≅ ΔCOB. So, ∠AOB=∠COB (CPCT). Since ∠AOB+∠COB=180° (linear pair), 2∠AOB=180° => ∠AOB=90°. (Proved)
3. Diagonal AC of a parallelogram ABCD bisects ∠A. Show that (i) it bisects ∠C also, (ii) ABCD is a rhombus.
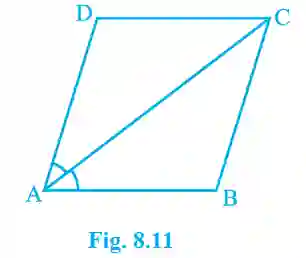 >
>Given: Parallelogram ABCD, AC bisects ∠A, so ∠DAC = ∠BAC.
(i) Show it bisects ∠C:
Since AB || DC, ∠BAC = ∠DCA (alternate interior angles).
Since AD || BC, ∠DAC = ∠BCA (alternate interior angles).
Given ∠DAC = ∠BAC, it follows that ∠DCA = ∠BCA. Thus, AC bisects ∠C.
(ii) Show ABCD is a rhombus:
In ΔABC, we have ∠BAC = ∠BCA (proved above).
Sides opposite to equal angles are equal, so BC = AB.
A parallelogram with adjacent sides equal is a rhombus.
(Proved)
4. ABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that: (i) ABCD is a square (ii) diagonal BD bisects ∠B as well as ∠D.
(i) Show ABCD is a square:
Given AC bisects ∠C, so ∠DCA = ∠BCA. Also, ∠BCA = ∠DAC (alternate interior angles).
Therefore, in ΔADC, ∠DCA = ∠DAC. Sides opposite to equal angles are equal, so AD=DC.
A rectangle with adjacent sides equal is a square.
(ii) Show BD bisects ∠B and ∠D:
Since ABCD is now a square, all sides are equal. In ΔBCD, BC=CD.
Therefore, ∠CDB = ∠CBD (angles opposite equal sides).
Also, ∠CDB = ∠ABD (alternate interior angles).
So, ∠CBD = ∠ABD, which means BD bisects ∠B. Similarly, BD bisects ∠D.
(Proved)
5. In parallelogram ABCD, two points P and Q are taken on diagonal BD such that DP = BQ. Show that:
 >
>(i) ΔAPD ≅ ΔCQB:
In ΔAPD and ΔCQB: AD=CB (opp. sides of ||gm), DP=BQ (given), ∠ADP=∠CBQ (alt. int. angles). By SAS, ΔAPD ≅ ΔCQB.
(ii) AP = CQ:
Since ΔAPD ≅ ΔCQB, AP = CQ by CPCT.
(iii) ΔAQB ≅ ΔCPD:
In ΔAQB and ΔCPD: AB=CD (opp. sides of ||gm), BQ=DP (given), ∠ABQ=∠CDP (alt. int. angles). By SAS, ΔAQB ≅ ΔCPD.
(iv) AQ = CP:
Since ΔAQB ≅ ΔCPD, AQ = CP by CPCT.
(v) APCQ is a parallelogram:
From (ii) and (iv), we have AP=CQ and AQ=CP. Since both pairs of opposite sides are equal, APCQ is a parallelogram.
(Proved)
6. ABCD is a parallelogram and AP and CQ are perpendiculars from vertices A and C on diagonal BD. Show that (i) ΔAPB ≅ ΔCQD (ii) AP = CQ.
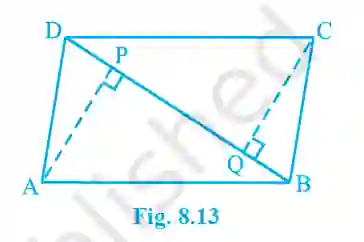 >
>(i) Show ΔAPB ≅ ΔCQD:
In ΔAPB and ΔCQD:
• ∠APB = ∠CQD = 90° (Given)
• AB = CD (Opposite sides of a parallelogram)
• ∠ABP = ∠CDQ (Alternate interior angles, since AB || DC)
By AAS congruence rule, ΔAPB ≅ ΔCQD.
(ii) Show AP = CQ:
Since ΔAPB ≅ ΔCQD, their corresponding parts are equal. Therefore, AP = CQ by CPCT.
(Proved)
7. ABCD is a trapezium in which AB || CD and AD = BC. Show that: (i) ∠A = ∠B (ii) ∠C = ∠D (iii) ΔABC ≅ ΔBAD (iv) diagonal AC = diagonal BD.
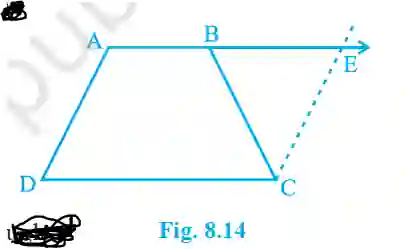 >
>Hint: Extend AB and draw a line through C parallel to DA intersecting AB produced at E.
Proof:
By construction, AECD is a parallelogram. So, AD=CE. Given AD=BC, so CE=BC.
In ΔBCE, since CE=BC, ∠CBE = ∠CEB. Also ∠A + ∠CEB = 180° (co-interior).
And ∠B + ∠CBE = 180° (linear pair). Since ∠CBE = ∠CEB, it implies ∠A = ∠B. (i) Proved.
Since AB || DC, ∠A+∠D=180° and ∠B+∠C=180°. As ∠A=∠B, it follows that ∠C=∠D. (ii) Proved.
In ΔABC and ΔBAD: AB=BA (common), BC=AD (given), ∠ABC=∠BAD (proved). By SAS, ΔABC ≅ ΔBAD. (iii) Proved.
Since ΔABC ≅ ΔBAD, their corresponding parts are equal. So, AC = BD. (iv) Proved.