Exercise 10.2 Solutions
Circles
1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is…
Let the center of the circle be O and the point of tangency be T. The radius OT is perpendicular to the tangent QT, forming a right-angled triangle ΔOTQ.
Given: QT (Tangent) = 24 cm, OQ (Hypotenuse) = 25 cm.
By Pythagoras theorem: OT² + QT² = OQ².
OT² + 24² = 25²
OT² + 576 = 625
OT² = 625 – 576 = 49
OT = √49 = 7 cm.
Answer: (A) 7 cm.
2. In Fig. 10.11, if TP and TQ are the two tangents to a circle with centre O so that ∠POQ = 110°, then ∠PTQ is equal to…
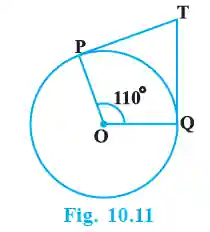 >
>In the quadrilateral OPTQ, the sum of all angles is 360°.
The radius is perpendicular to the tangent at the point of contact. So, ∠OPT = 90° and ∠OQT = 90°.
Given ∠POQ = 110°.
So, ∠OPT + ∠OQT + ∠POQ + ∠PTQ = 360°.
90° + 90° + 110° + ∠PTQ = 360°
290° + ∠PTQ = 360°
∠PTQ = 360° – 290° = 70°.
Answer: (B) 70°.
3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to…
Given ∠APB = 80°. The line joining the center to the external point bisects the angle between the tangents. So, ∠APO = ∠BPO = 80°/2 = 40°.
The radius OA is perpendicular to the tangent PA, so ∠OAP = 90°.
In right-angled triangle ΔOAP, the sum of angles is 180°.
∠POA + ∠OAP + ∠APO = 180°
∠POA + 90° + 40° = 180°
∠POA + 130° = 180°
∠POA = 50°.
Answer: (A) 50°.
4. Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Let AB be a diameter of a circle with center O. Let PQ and RS be the tangents drawn at points A and B respectively.
The radius OA is perpendicular to the tangent PQ at point A. So, ∠OAP = 90°.
The radius OB is perpendicular to the tangent RS at point B. So, ∠OBS = 90°.
Since AB is a straight line, ∠OAP and ∠OBS are alternate interior angles for the lines PQ and RS with transversal AB.
As ∠OAP = ∠OBS = 90°, the alternate interior angles are equal. Therefore, the lines PQ and RS are parallel. (Proved)
5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Let AB be a tangent to a circle with center O at point P. We need to prove that the perpendicular to AB at P passes through O.
We know that the radius OP is perpendicular to the tangent AB at P (i.e., ∠OPB = 90°).
Let’s assume there is another line, XP, which is perpendicular to AB at P, but does not pass through O. Then ∠XPB = 90°.
This implies ∠OPB = ∠XPB = 90°, which is only possible if the line segment OP and XP coincide.
This contradicts our assumption that XP does not pass through O. Thus, our assumption was wrong.
Therefore, the perpendicular at the point of contact to the tangent must pass through the centre. (Proved)
6. The length of a tangent from a point A at distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Let the center be O and point of tangency be T. In right-angled ΔOTA:
Distance from center, OA (Hypotenuse) = 5 cm.
Length of tangent, AT = 4 cm.
By Pythagoras theorem: OT² + AT² = OA².
Radius² + 4² = 5² => Radius² + 16 = 25 => Radius² = 9 => Radius = 3 cm.
Answer: The radius is 3 cm.
7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Let the center be O. Let AB be the chord of the larger circle that is tangent to the smaller circle at point P.
OP is the radius of the smaller circle (OP = 3 cm) and OA is the radius of the larger circle (OA = 5 cm).
The radius OP is perpendicular to the tangent chord AB. In the right-angled ΔOPA:
OP² + AP² = OA² => 3² + AP² = 5² => 9 + AP² = 25 => AP² = 16 => AP = 4 cm.
The perpendicular from the center bisects the chord, so AB = 2 × AP = 2 × 4 = 8 cm.
Answer: The length of the chord is 8 cm.
8. A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC.
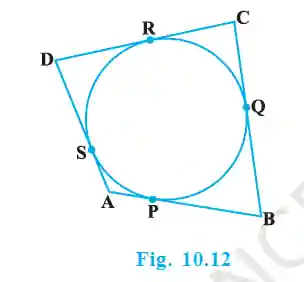 >
>Let the points of contact on sides AB, BC, CD, DA be P, Q, R, S respectively.
We know that tangents from an external point to a circle are equal in length.
From point A: AP = AS —(1)
From point B: BP = BQ —(2)
From point C: CR = CQ —(3)
From point D: DR = DS —(4)
Adding all four equations:
(AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
Using the diagram, this simplifies to:
AB + CD = AD + BC. (Proved)
9. In Fig. 10.13, XY and X′Y′ are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting XY at A and X′Y′ at B. Prove that ∠AOB = 90°.
 >
>Join OC. In ΔOPA and ΔOCA:
OP = OC (Radii of the same circle)
OA = OA (Common side)
AP = AC (Tangents from external point A)
By SSS congruence, ΔOPA ≅ ΔOCA. So, ∠POA = ∠COA by CPCT. Let this be x.
Similarly, in ΔOQB and ΔOCB:
OQ = OC (Radii), OB = OB (Common), BQ = BC (Tangents from B).
ΔOQB ≅ ΔOCB. So, ∠QOB = ∠COB by CPCT. Let this be y.
Since POQ is a straight line (diameter), ∠POQ = 180°.
∠POA + ∠COA + ∠COB + ∠QOB = 180°
x + x + y + y = 180° => 2x + 2y = 180° => x + y = 90°.
We need to find ∠AOB, which is ∠COA + ∠COB = x + y.
Therefore, ∠AOB = 90°. (Proved)
10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the centre.
Let the external point be P, and the tangents touch the circle at A and B. Let the center be O.
We need to prove that ∠APB + ∠AOB = 180°.
In the quadrilateral OAPB, the sum of angles is 360°.
The radius OA is perpendicular to tangent PA, so ∠OAP = 90°.
The radius OB is perpendicular to tangent PB, so ∠OBP = 90°.
Sum of angles: ∠OAP + ∠OBP + ∠APB + ∠AOB = 360°.
90° + 90° + ∠APB + ∠AOB = 360°
180° + ∠APB + ∠AOB = 360°
∠APB + ∠AOB = 180°. (Proved)
11. Prove that the parallelogram circumscribing a circle is a rhombus.
Let ABCD be a parallelogram circumscribing a circle. Opposite sides are equal: AB = CD and BC = AD.
From the theorem that tangents from an external point are equal, we have:
AP = AS, BP = BQ, CR = CQ, DR = DS.
We know AB + CD = AD + BC (from Q8).
Since AB = CD and BC = AD, we can substitute:
AB + AB = BC + BC => 2AB = 2BC => AB = BC.
Since adjacent sides of the parallelogram are equal (AB = BC), it must be a rhombus. (Proved)
12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
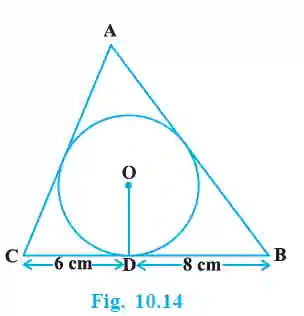 >
>Let the points of contact on AB and AC be E and F respectively.
CD = CF = 6 cm (Tangents from C).
BD = BE = 8 cm (Tangents from B).
Let AE = AF = x cm (Tangents from A).
The sides of the triangle are:
a = BC = 8 + 6 = 14 cm.
b = AC = x + 6 cm.
c = AB = x + 8 cm.
Semi-perimeter s = (a+b+c)/2 = (14 + x+6 + x+8)/2 = (28+2x)/2 = 14+x.
Area of ΔABC (Heron’s Formula) = √(s(s-a)(s-b)(s-c))
= √((14+x)(14+x-14)(14+x-(x+6))(14+x-(x+8))) = √((14+x)(x)(8)(6)) = √(48x(14+x)).
Also, Area of ΔABC = Area(ΔOBC) + Area(ΔOCA) + Area(ΔOAB)
= (1/2 × BC × r) + (1/2 × AC × r) + (1/2 × AB × r)
= 1/2 × 4 × (BC + AC + AB) = 2 × (2s) = 4s = 4(14+x).
Equate the two areas: √(48x(14+x)) = 4(14+x).
Squaring both sides: 48x(14+x) = 16(14+x)².
Divide by 16(14+x): 3x = 14+x => 2x=14 => x=7 cm.
AB = x + 8 = 7 + 8 = 15 cm.
AC = x + 6 = 7 + 6 = 13 cm.
Answer: AB = 15 cm, AC = 13 cm.
13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Let quadrilateral ABCD circumscribe a circle with center O, touching sides at P, Q, R, S. Join OA, OB, OC, OD, OP, OQ, OR, OS.
In ΔOAP and ΔOAS:
OP = OS (Radii), OA = OA (Common), AP = AS (Tangents from A).
By SSS, ΔOAP ≅ ΔOAS. So ∠AOP = ∠AOS. Let’s call this ∠1.
Similarly, ∠BOP = ∠BOQ = ∠2, ∠COQ = ∠COR = ∠3, ∠DOR = ∠DOS = ∠4.
The sum of all angles at the center O is 360°.
2∠1 + 2∠2 + 2∠3 + 2∠4 = 360° => ∠1+∠2+∠3+∠4 = 180°.
Angle subtended by side AB is ∠AOB = ∠1+∠2.
Angle subtended by opposite side CD is ∠COD = ∠3+∠4.
Sum = ∠AOB + ∠COD = (∠1+∠2) + (∠3+∠4) = 180°.
Similarly, ∠BOC + ∠DOA = 180°. Thus, opposite sides subtend supplementary angles at the center. (Proved)


