Exercise 6.2 Solutions
Triangles
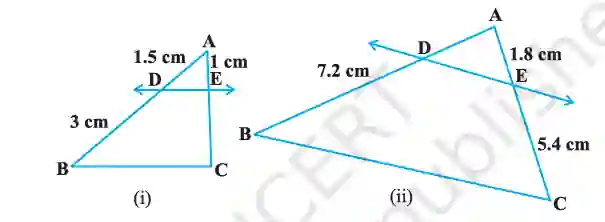
1. In Fig. 6.17, (i) and (ii), DE || BC. Find EC in (i) and AD in (ii).
 >
>We use the Basic Proportionality Theorem (BPT), which states that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided in the same ratio.
(i) Given: AD = 1.5 cm, DB = 3 cm, AE = 1 cm, DE || BC.
By BPT, ADDB = AEEC.
1.53 = 1EC => 12 = 1EC => EC = 2 cm.
(ii) Given: DB = 7.2 cm, AE = 1.8 cm, EC = 5.4 cm, DE || BC.
By BPT, ADDB = AEEC.
AD7.2 = 1.85.4 => AD7.2 = 13 => AD = 7.2 / 3 = 2.4 cm.
2. E and F are points on the sides PQ and PR respectively of a ΔPQR. For each of the following cases, state whether EF || QR.
We use the Converse of BPT, which states that if a line divides any two sides of a triangle in the same ratio, then the line is parallel to the third side.
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
Ratio PEEQ = 3.93 = 1.3.
Ratio PFFR = 3.62.4 = 1.5.
Since the ratios are not equal, EF is not parallel to QR.
(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
Ratio PEQE = 44.5 = 89.
Ratio PFRF = 89.
Since the ratios are equal, EF is parallel to QR.
(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm
EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm.
FR = PR – PF = 2.56 – 0.36 = 2.20 cm.
Ratio PEEQ = 0.181.10 = 955.
Ratio PFFR = 0.362.20 = 955.
Since the ratios are equal, EF is parallel to QR.
3. In Fig. 6.18, if LM || CB and LN || CD, prove that AMAB = ANAD.
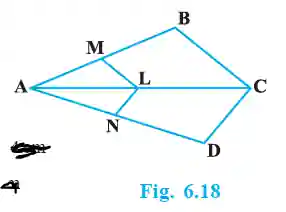 >
>Step 1: Apply BPT in ΔABC.
Given LM || CB. By BPT, AMMB = ALLC.
By corollary of BPT, we can also write AMAB = ALAC. —(1)
Step 2: Apply BPT in ΔADC.
Given LN || CD. By BPT, ANND = ALLC.
By corollary of BPT, we can also write ANAD = ALAC. —(2)
Step 3: Combine the results.
From equations (1) and (2), we see that both ratios are equal to ALAC.
Therefore, AMAB = ANAD. (Proved)
4. In Fig. 6.19, DE || AC and DF || AE. Prove that BFFE = BEEC.
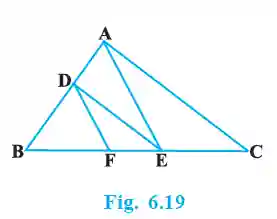 >
>Step 1: Apply BPT in ΔABC.
Given DE || AC. By BPT, BDDA = BEEC. —(1)
Step 2: Apply BPT in ΔABE.
Given DF || AE. By BPT, BDDA = BFFE. —(2)
Step 3: Combine the results.
From equations (1) and (2), we have:
BFFE = BEEC. (Proved)
5. In Fig. 6.20, DE || OQ and DF || OR. Show that EF || QR.
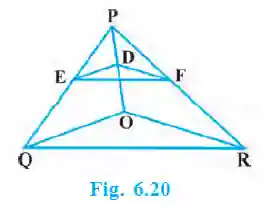 >
>Step 1: Apply BPT in ΔPOQ.
Given DE || OQ. By BPT, PEEQ = PDDO. —(1)
Step 2: Apply BPT in ΔPOR.
Given DF || OR. By BPT, PFFR = PDDO. —(2)
Step 3: Combine the results and apply Converse of BPT.
From (1) and (2), we get PEEQ = PFFR.
Now, in ΔPQR, since the line EF divides the sides PQ and PR in the same ratio, by the Converse of BPT, we can conclude that EF || QR. (Proved)
6. In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.
 >
>Step 1: Apply BPT in ΔOPQ.
Given AB || PQ. By BPT, OAAP = OBBQ. —(1)
Step 2: Apply BPT in ΔOPR.
Given AC || PR. By BPT, OAAP = OCCR. —(2)
Step 3: Combine and apply Converse of BPT.
From (1) and (2), we get OBBQ = OCCR.
Now, in ΔOQR, since the line BC divides the sides OQ and OR in the same ratio, by the Converse of BPT, we have BC || QR. (Proved)
7. Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Given: ΔABC, D is the mid-point of AB (so AD = DB). A line through D is parallel to BC and intersects AC at E (DE || BC).
To Prove: E is the mid-point of AC (i.e., AE = EC).
Proof: In ΔABC, since DE || BC, by Theorem 6.1 (BPT), we have:
ADDB = AEEC.
Since D is the mid-point of AB, AD = DB. So, ADDB = 1.
Therefore, AEEC = 1, which implies AE = EC.
This means E is the mid-point of AC. (Proved)
8. Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Given: ΔABC, D and E are the mid-points of sides AB and AC respectively.
To Prove: DE || BC.
Proof: Since D is the mid-point of AB, AD = DB, so ADDB = 1. —(1)
Since E is the mid-point of AC, AE = EC, so AEEC = 1. —(2)
From (1) and (2), we have ADDB = AEEC.
By Theorem 6.2 (Converse of BPT), since the line DE divides the sides AB and AC in the same ratio, DE must be parallel to the third side BC. (Proved)
9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that AOBO = CODO.
Given: Trapezium ABCD with AB || DC.
Construction: Draw a line EO through O, such that EO || AB || DC, where E is on AD.
Proof: In ΔADC, we have EO || DC. By BPT:
AEED = AOCO. —(1)
In ΔADB, we have EO || AB. By BPT:
AEED = BODO. —(2)
From (1) and (2):
AOCO = BODO.
Rearranging the terms by cross-multiplication gives:
AOBO = CODO. (Proved)
10. The diagonals of a quadrilateral ABCD intersect each other at the point O such that AOBO = CODO. Show that ABCD is a trapezium.
Given: Quadrilateral ABCD with AOBO = CODO.
Rearranging the given ratio: AOCO = BODO. —(1)
Construction: Draw a line EO through O such that EO || AB, intersecting AD at E.
Proof: In ΔDAB, since EO || AB, by BPT:
DEEA = DOBO. —(2)
From the given rearranged ratio (1), we have BODO = COAO. Taking the reciprocal gives DOBO = AOCO.
Substituting this into (2): DEEA = COAO.
Now in ΔADC, we have established that DEEA = COAO. By the Converse of BPT, this implies that EO || DC.
Since we constructed EO || AB, and we have now proved EO || DC, it follows that AB || DC. A quadrilateral with one pair of parallel sides is a trapezium.
Answer: ABCD is a trapezium. (Proved)


