Exercise 7.1 Solutions
Coordinate Geometry
1. Find the distance between the following pairs of points:
Using the Distance Formula: d = √[(x₂ - x₁)² + (y₂ - y₁)²]
(i) (2, 3), (4, 1)
d = √[(4 – 2)² + (1 – 3)²] = √[2² + (-2)²] = √[4 + 4] = √8 = 2√2.
(ii) (−5, 7), (−1, 3)
d = √[(-1 – (-5))² + (3 – 7)²] = √[4² + (-4)²] = √[16 + 16] = √32 = 4√2.
(iii) (a, b), (−a, −b)
d = √[(-a – a)² + (-b – b)²] = √[(-2a)² + (-2b)²] = √[4a² + 4b²] = √[4(a² + b²)] = 2√(a² + b²).
2. Find the distance between the points (0, 0) and (36, 15).
Using the Distance Formula:
d = √[(36 – 0)² + (15 – 0)²] = √[36² + 15²] = √[1296 + 225] = √1521 = 39.
3. Determine if the points (1, 5), (2, 3) and (–2, –11) are collinear.
Points are collinear if the sum of the lengths of any two line segments is equal to the length of the third. Let A=(1,5), B=(2,3), C=(-2,-11).
AB = √[(2-1)² + (3-5)²] = √[1² + (-2)²] = √5.
BC = √[(-2-2)² + (-11-3)²] = √[(-4)² + (-14)²] = √[16 + 196] = √212.
AC = √[(-2-1)² + (-11-5)²] = √[(-3)² + (-16)²] = √[9 + 256] = √265.
Since AB + BC (√5 + √212) ≠ AC (√265), the points are not collinear.
Answer: The points are not collinear.
4. Check whether (5, –2), (6, 4) and (7, –2) are the vertices of an isosceles triangle.
Let A=(5,-2), B=(6,4), C=(7,-2). We find the lengths of the sides.
AB = √[(6-5)² + (4-(-2))²] = √[1² + 6²] = √37.
BC = √[(7-6)² + (-2-4)²] = √[1² + (-6)²] = √37.
AC = √[(7-5)² + (-2-(-2))²] = √[2² + 0²] = √4 = 2.
Since two sides AB and BC are equal (√37), the triangle is isosceles.
Answer: Yes, they are the vertices of an isosceles triangle.
5. In a classroom, 4 friends are seated at the points A, B, C and D… Using distance formula, find which of them is correct.
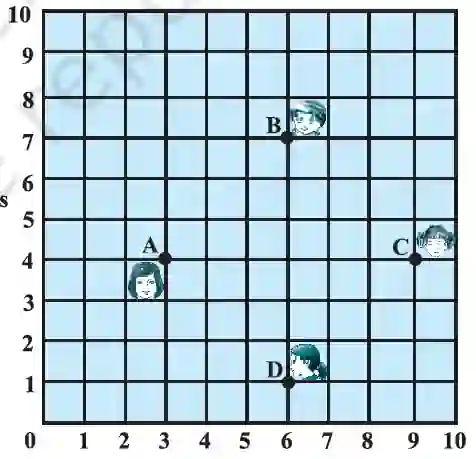 >
>From the figure, the coordinates are A(3,4), B(6,7), C(9,4), and D(6,1).
Step 1: Calculate the lengths of the four sides.
AB = √[(6-3)² + (7-4)²] = √[3² + 3²] = √18 = 3√2.
BC = √[(9-6)² + (4-7)²] = √[3² + (-3)²] = √18 = 3√2.
CD = √[(6-9)² + (1-4)²] = √[(-3)² + (-3)²] = √18 = 3√2.
DA = √[(3-6)² + (4-1)²] = √[(-3)² + 3²] = √18 = 3√2.
All four sides are equal.
Step 2: Calculate the lengths of the diagonals.
AC = √[(9-3)² + (4-4)²] = √[6² + 0²] = 6.
BD = √[(6-6)² + (1-7)²] = √[0² + (-6)²] = 6.
The diagonals are also equal.
Since all four sides are equal and the diagonals are equal, ABCD is a square.
Answer: Champa is correct.
6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:
(i) (–1, –2), (1, 0), (–1, 2), (–3, 0)
Let A(-1,-2), B(1,0), C(-1,2), D(-3,0).
AB=√(2²+2²)=√8. BC=√((-2)²+2²)=√8. CD=√((-2)²+(-2)²)=√8. DA=√((-2)²+(-2)²)=√8. All sides are equal.
Diagonals: AC=√(0²+4²)=4. BD=√((-4)²+0²)=4.
Since all sides are equal and diagonals are equal, it is a Square.
(ii) (–3, 5), (3, 1), (0, 3), (–1, –4)
Let A(-3,5), B(3,1), C(0,3), D(-1,-4).
AB=√52, BC=√13, AC=√13.
Here, BC + AC = √13 + √13 = 2√13 = √52 = AB.
Since AC + CB = AB, the points A, C, and B are collinear. The four points cannot form a quadrilateral.
Answer: Not a quadrilateral.
(iii) (4, 5), (7, 6), (4, 3), (1, 2)
Let A(4,5), B(7,6), C(4,3), D(1,2).
AB=√10, BC=√18, CD=√10, DA=√18. Opposite sides are equal (AB=CD, BC=DA).
Diagonals: AC=√4=2, BD=√52. Diagonals are not equal.
Since opposite sides are equal and diagonals are not, it is a Parallelogram.
7. Find the point on the x-axis which is equidistant from (2, –5) and (–2, 9).
Let the point on the x-axis be P(x, 0). Let the given points be A(2,-5) and B(-2,9).
Given PA = PB, so PA² = PB².
(x – 2)² + (0 – (-5))² = (x – (-2))² + (0 – 9)²
(x – 2)² + 5² = (x + 2)² + (-9)²
x² – 4x + 4 + 25 = x² + 4x + 4 + 81
-4x + 29 = 4x + 85
-8x = 56 => x = -7.
Answer: The point is (-7, 0).
8. Find the values of y for which the distance between the points P(2, –3) and Q(10, y) is 10 units.
Given distance PQ = 10. So, PQ² = 100.
(10 – 2)² + (y – (-3))² = 100
8² + (y + 3)² = 100
64 + (y + 3)² = 100
(y + 3)² = 36
y + 3 = ±6.
Case 1: y + 3 = 6 => y = 3.
Case 2: y + 3 = -6 => y = -9.
Answer: The values of y are 3 and -9.
9. If Q(0, 1) is equidistant from P(5, –3) and R(x, 6), find the values of x. Also find the distances QR and PR.
Given QP = QR, so QP² = QR².
(5 – 0)² + (-3 – 1)² = (x – 0)² + (6 – 1)²
5² + (-4)² = x² + 5²
25 + 16 = x² + 25 => x² = 16 => x = ±4.
Case 1: x = 4. R is (4,6).
QR = √[(4-0)² + (6-1)²] = √[16 + 25] = √41.
PR = √[(4-5)² + (6-(-3))²] = √[(-1)² + 9²] = √82.
Case 2: x = -4. R is (-4,6).
QR = √[(-4-0)² + (6-1)²] = √[16 + 25] = √41.
PR = √[(-4-5)² + (6-(-3))²] = √[(-9)² + 9²] = √[81+81] = √162 = 9√2.
10. Find a relation between x and y such that the point (x, y) is equidistant from the point (3, 6) and (–3, 4).
Let P(x,y), A(3,6), B(-3,4). Given PA = PB, so PA² = PB².
(x – 3)² + (y – 6)² = (x – (-3))² + (y – 4)²
(x² – 6x + 9) + (y² – 12y + 36) = (x² + 6x + 9) + (y² – 8y + 16)
Cancel x² and y² from both sides:
-6x – 12y + 45 = 6x – 8y + 25
Bring all terms to one side:
0 = 12x + 4y – 20
Divide by 4: 3x + y – 5 = 0.
Answer: The relation is 3x + y – 5 = 0.


