Exercise 9.1 Solutions
Some Applications of Trigonometry
1. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
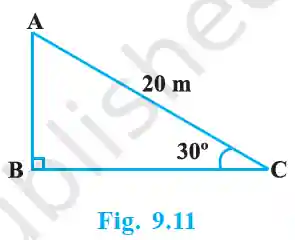 >
>Let AB be the pole and AC be the rope. In ΔABC:
Given: AC (Hypotenuse) = 20 m, ∠C = 30°.
We need to find the height of the pole, AB (Opposite).
Using sin: sin θ = Opposite/Hypotenuse = AB/AC.
sin 30° = AB / 20.
1/2 = AB / 20 => AB = 20 / 2 = 10 m.
Answer: The height of the pole is 10 m.
2. A tree breaks due to storm and the broken part bends so that the top of the tree touches the ground making an angle 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Let the tree be initially at height (AB + AC). It breaks at A, and the top C touches the ground at C’.
In right ΔABC’: BC’ (Adjacent) = 8 m, ∠AC’B = 30°.
Height of tree = AB (standing part) + AC’ (broken part/hypotenuse).
Find standing part (AB): tan 30° = AB/BC’ => 1/√3 = AB/8 => AB = 8/√3 m.
Find broken part (AC’): cos 30° = BC’/AC’ => √3/2 = 8/AC’ => AC’ = 16/√3 m.
Total Height = AB + AC’ = 8/√3 + 16/√3 = 24/√3 = 8√3 m.
Answer: The height of the tree is 8√3 m.
3. A contractor plans to install two slides… What should be the length of the slide in each case?
Case 1: For younger children
Height (Opposite) = 1.5 m, Angle = 30°.
sin 30° = Height / Length => 1/2 = 1.5 / Length => Length = 1.5 × 2 = 3 m.
Case 2: For elder children
Height (Opposite) = 3 m, Angle = 60°.
sin 60° = Height / Length => √3/2 = 3 / Length => Length = 6/√3 = 2√3 m.
Answer: Length of slides are 3 m and 2√3 m respectively.
4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Let AB be the tower. In ΔABC:
Distance BC (Adjacent) = 30 m, Angle ∠C = 30°.
tan 30° = AB/BC => 1/√3 = AB/30 => AB = 30/√3 = 10√3 m.
Answer: The height of the tower is 10√3 m.
5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string…
Height (Opposite) = 60 m, Angle = 60°.
sin 60° = Height / Length of string => √3/2 = 60 / Length => Length = 120/√3 = 40√3 m.
Answer: The length of the string is 40√3 m.
6. A 1.5 m tall boy is standing at some distance from a 30 m tall building… Find the distance he walked towards the building.
Height of building observed by boy = 30 – 1.5 = 28.5 m.
Let initial distance be D and final distance be d.
In the first case (angle 30°): tan 30° = 28.5 / D => 1/√3 = 28.5 / D => D = 28.5√3 m.
In the second case (angle 60°): tan 60° = 28.5 / d => √3 = 28.5 / d => d = 28.5/√3 m.
Distance walked = D – d = 28.5√3 – 28.5/√3 = 28.5(√3 – 1/√3) = 28.5(2/√3) = 57/√3 = 19√3 m.
Answer: The distance he walked is 19√3 m.
7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Let building height BC=20m, tower height CD=h. Distance from point A to base=AB.
In ΔABC: tan 45° = BC/AB => 1 = 20/AB => AB = 20 m.
In ΔABD: tan 60° = BD/AB = (BC+CD)/AB => √3 = (20+h)/20.
20√3 = 20 + h => h = 20√3 – 20 = 20(√3 – 1) m.
Answer: The height of the tower is 20(√3 – 1) m.
8. A statue, 1.6 m tall, stands on the top of a pedestal… Find the height of the pedestal.
Let pedestal height BC=h, statue height CD=1.6m. Distance from point A to base=AB.
In ΔABC: tan 45° = BC/AB => 1 = h/AB => AB = h.
In ΔABD: tan 60° = BD/AB = (h+1.6)/h => √3 = (h+1.6)/h.
h√3 = h + 1.6 => h(√3 – 1) = 1.6 => h = 1.6/(√3 – 1) = 0.8(√3 + 1) m.
Answer: The height of the pedestal is 0.8(√3 + 1) m.
9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building.
Let building height be h, tower height be H=50m. Let distance between them be x.
From foot of building to top of tower: tan 60° = H/x => √3 = 50/x => x = 50/√3 m.
From foot of tower to top of building: tan 30° = h/x => 1/√3 = h/(50/√3) => 1/√3 = h√3/50.
50 = 3h => h = 50/3 m.
Answer: The height of the building is 50/3 m.
10. Two poles of equal heights are standing opposite each other on either side of the road, which is 80 m wide… Find the height of the poles and the distances of the point from the poles.
Let height of poles be h. Let the point be x m from one pole, so it is (80-x) m from the other.
From the first triangle: tan 60° = h/x => h = x√3.
From the second triangle: tan 30° = h/(80-x) => h = (80-x)/√3.
Equating h: x√3 = (80-x)/√3 => 3x = 80-x => 4x = 80 => x = 20 m.
Height h = 20√3 m.
The other distance is 80-20 = 60 m.
Answer: Height of poles is 20√3 m. The distances are 20 m and 60 m.
11. A TV tower stands vertically on a bank of a canal… Find the height of the tower and the width of the canal.
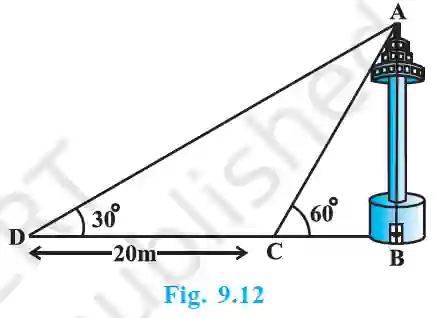 >
>Let tower height be h and canal width be x. In ΔABC:
tan 60° = h/x => h = x√3.
From point D, distance is x+20. In ΔABD:
tan 30° = h/(x+20) => h = (x+20)/√3.
Equating h: x√3 = (x+20)/√3 => 3x = x+20 => 2x = 20 => x = 10 m.
Height h = 10√3 m.
Answer: Height is 10√3 m, width is 10 m.
12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Let building be AB=7m, tower be CD. Let horizontal distance be x.
Angle of depression to foot (D): tan 45° = AB/BD_horizontal = 7/x => 1 = 7/x => x=7m.
Let CE be the part of the tower above the building’s height. In the upper triangle:
tan 60° = CE/x => √3 = CE/7 => CE = 7√3 m.
Total height of tower = CD = CE + ED = 7√3 + 7 = 7(√3 + 1) m.
Answer: The height of the tower is 7(√3 + 1) m.
13. As observed from the top of a 75 m high lighthouse from the sea-level, the angles of depression of two ships are 30° and 45°… Find the distance between the two ships.
Let lighthouse be AB=75m. Let ships be at C and D.
For ship at C (angle 45°): tan 45° = AB/BC => 1 = 75/BC => BC = 75 m.
For ship at D (angle 30°): tan 30° = AB/BD => 1/√3 = 75/BD => BD = 75√3 m.
Distance between ships = CD = BD – BC = 75√3 – 75 = 75(√3 – 1) m.
Answer: The distance is 75(√3 – 1) m.
14. A 1.2 m tall girl spots a balloon moving with the wind… Find the distance travelled by the balloon during the interval.
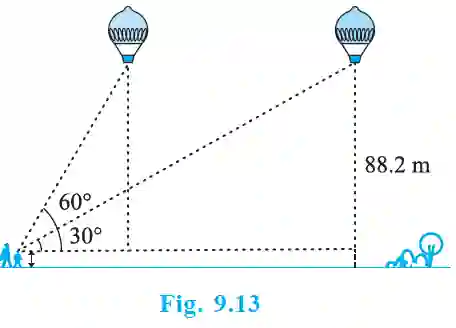 >
>Height of balloon from girl’s eye level = 88.2 – 1.2 = 87 m.
Let initial horizontal distance be D, final be d.
tan 60° = 87/D => √3 = 87/D => D = 87/√3 = 29√3 m.
tan 30° = 87/d => 1/√3 = 87/d => d = 87√3 m.
Distance travelled by balloon = d – D = 87√3 – 29√3 = 58√3 m.
Answer: The distance travelled is 58√3 m.
15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Let tower height be h. Let car be at C (angle 30°) then at D (angle 60°).
In ΔABD: tan 60° = h/BD => h = BD√3.
In ΔABC: tan 30° = h/BC = h/(BD+CD) => h = (BD+CD)/√3.
Equating h: BD√3 = (BD+CD)/√3 => 3BD = BD+CD => 2BD = CD.
This means the distance CD is twice the distance BD.
Time taken to cover CD = 6 seconds.
Since speed is uniform, time taken to cover BD (half the distance of CD) will be half the time.
Time to cover BD = 6 / 2 = 3 seconds.
Answer: The time taken is 3 seconds.
16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Let tower height be h. Let the two points be at distances 4m and 9m. Let the angles be θ and (90-θ).
From point at 9m: tan θ = h/9 —(1)
From point at 4m: tan(90-θ) = h/4 => cot θ = h/4 —(2)
Multiply eq (1) and (2): tan θ × cot θ = (h/9) × (h/4).
1 = h²/36 => h² = 36 => h = 6 m.
(Proved)


