Exercise 6.2 Solutions (Class 9)
Lines and Angles
1. In Fig. 6.23, if AB || CD, CD || EF and y : z = 3 : 7, find x.
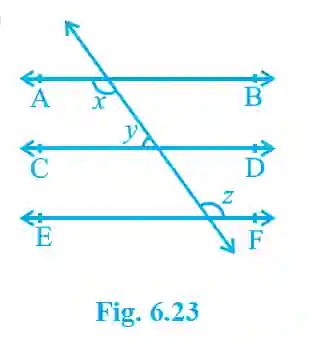 >
>Since AB || CD and CD || EF, then lines parallel to the same line are parallel to each other. Therefore, AB || EF.
Now, since AB || EF, angles x and z are alternate interior angles. Thus, x = z. —(1)
Also, since AB || CD, angles x and y are consecutive interior angles (angles on the same side of the transversal). Their sum is 180°.
So, x + y = 180°.
Substitute x = z from equation (1) into this equation: z + y = 180°.
We are given the ratio y : z = 3 : 7. Let y = 3a and z = 7a.
Substitute these values: 3a + 7a = 180° => 10a = 180° => a = 18°.
Now, find the value of z: z = 7a = 7 × 18° = 126°.
Since x = z, the value of x is also 126°.
Answer: x = 126°.
2. In Fig. 6.24, if AB || CD, EF ⊥ CD and ∠GED = 126°, find ∠AGE, ∠GEF and ∠FGE.
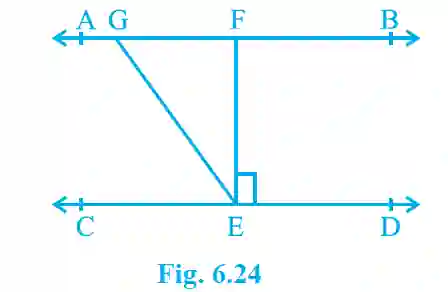 >
>Find ∠AGE:
Since AB || CD, ∠AGE and ∠GED are alternate interior angles.
Given ∠GED = 126°, so ∠AGE = 126°.
Find ∠GEF:
We are given EF ⊥ CD, which means ∠FED = 90°.
From the figure, we see that ∠GED = ∠GEF + ∠FED.
126° = ∠GEF + 90° => ∠GEF = 36°.
Find ∠FGE:
Since AB is a straight line, ∠AGE and ∠FGE form a linear pair. Their sum is 180°.
∠AGE + ∠FGE = 180°.
126° + ∠FGE = 180° => ∠FGE = 54°.
3. In Fig. 6.25, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
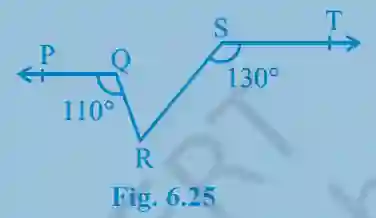 >
>Hint: Draw a line parallel to ST through point R.
Construction: Draw a line XRY through point R such that it is parallel to ST. Since PQ || ST, then XRY is also parallel to PQ.
First, consider PQ || XRY and the transversal QR. The angle supplementary to ∠PQR (which is 180° – 110° = 70°) and ∠QRX are alternate interior angles.
So, ∠QRX = 70°.
Next, consider ST || XRY and the transversal SR. The angle supplementary to ∠RST (which is 180° – 130° = 50°) and ∠SRY are alternate interior angles.
So, ∠SRY = 50°.
Since XRY is a straight line, the sum of angles on it is 180°.
∠QRX + ∠QRS + ∠SRY = 180°.
70° + ∠QRS + 50° = 180°.
120° + ∠QRS = 180°.
∠QRS = 180° - 120° = 60°.
Answer: ∠QRS = 60°.
4. In Fig. 6.26, if AB || CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.
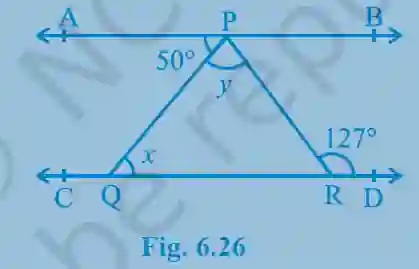 >
>Since AB || CD and PQ is the transversal, the angles ∠APQ and ∠PQR (x) are alternate interior angles.
Therefore, x = 50°.
Again, since AB || CD and PR is the transversal, the angles ∠APR and ∠PRD are alternate interior angles.
So, ∠APR = ∠PRD = 127°.
From the figure, we can see that ∠APR is the sum of ∠APQ and ∠QPR (y).
∠APR = ∠APQ + y.
127° = 50° + y.
y = 127° - 50° = 77°.
Answer: x = 50°, y = 77°.
5. In Fig. 6.27, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C, and again reflects back along CD. Prove that AB || CD.
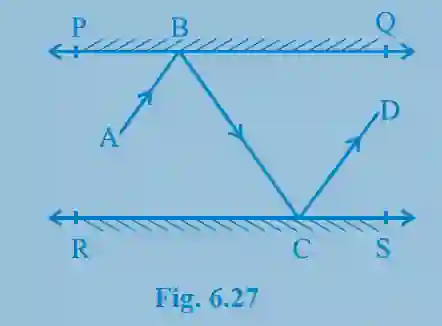 >
>Construction: At the point of incidence B, draw a normal BM ⊥ PQ. At the point of incidence C, draw a normal CN ⊥ RS.
Proof:
Since PQ || RS, their respective normals must also be parallel to each other. So, BM || CN.
By the law of reflection, the angle of incidence is equal to the angle of reflection.
Therefore, ∠ABM = ∠MBC (let’s call this ∠1 = ∠2).
And, ∠BCN = ∠NCD (let’s call this ∠3 = ∠4).
Now, since BM || CN and BC is a transversal line, the alternate interior angles are equal.
So, ∠MBC = ∠BCN (which means ∠2 = ∠3).
From our equations, we get: ∠1 = ∠2 = ∠3 = ∠4.
The total angle ∠ABC = ∠1 + ∠2 = 2 * ∠2.
The total angle ∠BCD = ∠3 + ∠4 = 2 * ∠3.
Since ∠2 = ∠3, it follows that 2 * ∠2 = 2 * ∠3, which means ∠ABC = ∠BCD.
For the lines AB and CD, with BC as the transversal, we have shown that the alternate interior angles (∠ABC and ∠BCD) are equal. When alternate interior angles are equal, the lines are parallel.
Thus, AB || CD. (Proved)



