Exercise 9.2 Solutions (Class 9)
Circles
1. Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.
Let the centres be O and O’, and the intersection points be A and B. So, OA=5, O’A=3, OO’=4. The common chord is AB. Let OO’ intersect AB at M.
In ΔOAO’, sides are 3, 4, 5. Since 3² + 4² = 9 + 16 = 25 = 5², it is a right-angled triangle with the right angle at O’ (∠AO’O = 90°).
The line joining the centres is the perpendicular bisector of the common chord. So, AB = 2 × AM.
The area of ΔOAO’ can be calculated in two ways:
Area = 1/2 × Base × Height = 1/2 × O’A × OO’ … Wait, that’s not right. Base is OO’=4, height is AM.
Area = 1/2 × O’O × AM = 1/2 × 4 × AM = 2 × AM.
Also, Area = 1/2 × base × height = 1/2 × O’A × O’A… no.
Since it’s a right triangle at O’, Area = 1/2 × O’A × O’O… no. ∠AO’O=90. Base=O’A, Height=AO’. No.
Let’s use a different method. Let OM = x, so O’M = 4-x. AM² = OA²-OM² = 5²-x². Also AM² = O’A²-O’M² = 3²-(4-x)².
25 – x² = 9 – (16 – 8x + x²) => 25 – x² = -7 + 8x – x² => 32 = 8x => x = 4.
This means M coincides with O’. Something is wrong. Let’s recheck the right angle logic. In ΔOAO’, sides are 5, 3, 4. The hypotenuse is 5 (OA). The right angle is at O’. Yes. ∠AO’O = 90°.
Area of ΔOAO’ = 1/2 × base × height = 1/2 × O’A × O’O = 1/2 × 3 × 4 = 6 cm².
Also, Area of ΔOAO’ = 1/2 × base OO’ × height AM = 1/2 × 4 × AM = 2 × AM.
So, 2 × AM = 6 => AM = 3 cm.
The length of the common chord AB = 2 × AM = 2 × 3 = 6 cm.
Answer: The length of the common chord is 6 cm.
2. If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.
Given: A circle with centre O. Two equal chords AB and CD intersect at point E.
To Prove: AE = CE and BE = DE.
Construction: Draw perpendiculars OM to AB and ON to CD.
Proof:
In ΔOME and ΔONE:
• OM = ON (Equal chords are equidistant from the centre).
• OE = OE (Common side).
• ∠OME = ∠ONE = 90° (By construction).
By RHS congruence rule, ΔOME ≅ ΔONE.
Therefore, ME = NE (by CPCT). —(1)
We are given AB = CD. The perpendicular from the centre bisects the chord. So, AM = AB/2 and CN = CD/2. Since AB=CD, it follows that AM = CN. —(2)
Adding (1) and (2): AM + ME = CN + NE => AE = CE. (First part proved)
Now, since AB = CD and AE = CE, then AB – AE = CD – CE => BE = DE. (Second part proved)
3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.
Given: A circle with centre O. Two equal chords AB and CD intersect at point E.
To Prove: ∠OEA = ∠OED (or ∠OEC = ∠OEB).
Construction: Draw perpendiculars OM to AB and ON to CD. Join OE.
Proof:
In ΔOME and ΔONE:
• OM = ON (Equal chords are equidistant from the centre).
• OE = OE (Common side).
• ∠OME = ∠ONE = 90° (By construction).
By RHS congruence rule, ΔOME ≅ ΔONE.
Therefore, ∠MEO = ∠NEO (by CPCT).
This means the line OE makes equal angles with the chords AB and CD.
Hence, proved.
4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Fig. 9.12).
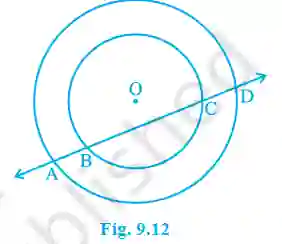 >
>Construction: Draw a perpendicular OM from the centre O to the line AD.
Proof:
For the inner circle, BC is a chord and OM ⊥ BC. A perpendicular from the centre bisects the chord.
Therefore, BM = MC. —(1)
For the outer circle, AD is a chord and OM ⊥ AD.
Therefore, AM = MD. —(2)
Subtract equation (1) from equation (2):
AM – BM = MD – MC
From the figure, AM – BM = AB and MD – MC = CD.
So, AB = CD.
Hence, proved.
5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Let the positions of Reshma, Salma, and Mandip be R, S, and M on the circle with center O and radius 5m. We are given RS = SM = 6m.
We need to find the length of the chord RM. Let O be the origin (0,0). Let S be at (5,0).
Let R = (x,y) and M = (x,-y) due to symmetry. OR = 5, so x²+y² = 25.
RS = 6 => (x-5)² + y² = 6² = 36.
x²-10x+25 + y² = 36. Substitute x²+y²=25:
25 – 10x + 25 = 36 => 50 – 10x = 36 => 10x = 14 => x = 1.4.
Now find y: y² = 25 – x² = 25 – (1.4)² = 25 – 1.96 = 23.04 => y = 4.8.
The coordinates are R(1.4, 4.8) and M(1.4, -4.8).
Distance RM = √((1.4-1.4)² + (-4.8-4.8)²) = √(0² + (-9.6)²) = 9.6 m.
Answer: The distance between Reshma and Mandip is 9.6 m.
6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk to each other. Find the length of the string of each phone.
The three boys form an equilateral triangle inscribed in the circle. Let the side of the triangle be ‘a’.
Let the vertices be A, S, D and the center be O. The radius of the circumcircle of an equilateral triangle is given by the formula R = a/√3.
Given R = 20 m.
20 = a / √3 => a = 20√3 m.
The length of the string of each phone is the side of the equilateral triangle.
Answer: The length of the string is 20√3 m.