Coulomb’s Law
Coulomb’s Law
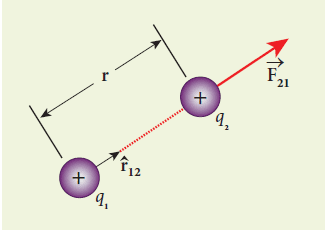
In 1786, Charles-Augustin de Coulomb deduced the expression for the force between two stationary point charges in a vacuum or free space. Consider two point charges, q1 and q2, at rest in a vacuum and separated by a distance r as shown in Figure 1.2. According to Coulomb, the force on the point charge q2 exerted by another point charge q1 is:
F = k (q1 q2 / r2) r̂12
where r̂12 is the unit vector directed from charge q1 to charge q2 and k is the proportionality constant.
Important Aspects of Coulomb’s Law
1. Proportionality of Forces
Coulomb’s law states that the electrostatic force is directly proportional to the product of the magnitudes of the two point charges and inversely proportional to the square of the distance between the two point charges.
2. Direction of Forces
The force on the charge q2 exerted by the charge q1 always lies along the line joining the two charges. r̂12 is the unit vector pointing from charge q1 to q2. Likewise, the force on the charge q1 exerted by q2 is along -r̂12 (i.e., in the direction opposite to r̂12).
3. Value of k in SI Units
In SI units, k = 1 / (4 π ε0) and its value is 9 × 109 N m2 C–2. Here, ε0 is the permittivity of free space or vacuum, and its value is:
ε0 = 8.854 × 10–12 C2 N–1 m–2
4. Electrostatic Force Magnitude
The magnitude of the electrostatic force between two charges, each of one coulomb, separated by a distance of 1 m is calculated as follows:
F = k (1 × 1 / 12) = 9 × 109 N
This is an enormous quantity, almost equivalent to the weight of one million tons. In practice, we never encounter charges of 1 coulomb. Most electrical phenomena involve charges of the order of microcoulombs (μC) or nanocoulombs (nC).
5. Coulomb’s Law in Different Mediums
In SI units, Coulomb’s law in a vacuum takes the form:
F = (1 / (4 π ε0)) (q1 q2 / r2) r̂12
In a medium of permittivity ε, the force between two point charges is given by:
F = (1 / (4 π ε)) (q1 q2 / r2) r̂12
Since ε > ε0, the force between two point charges in a medium other than a vacuum is always less than that in a vacuum. We define the relative permittivity for a given medium as εr = ε / ε0. For vacuum or air, εr = 1 and for all other media, εr > 1.
6. Comparison with Newton’s Law of Gravitation
Coulomb’s law has the same structure as Newton’s law of gravitation. Both are inversely proportional to the square of the distance between the particles. The electrostatic force is directly proportional to the product of the magnitudes of two point charges, while the gravitational force is directly proportional to the product of two masses. However, there are important differences:
- The gravitational force between two masses is always attractive, whereas the Coulomb force between two charges can be attractive or repulsive, depending on the nature of the charges.
- The value of the gravitational constant G = 6.67 × 10–11 N m2 kg–2. The value of the constant k in Coulomb’s law is 9 × 109 N m2 C–2. Since k is much greater than G, the electrostatic force is always greater in magnitude than the gravitational force for small objects.
- The gravitational force between two masses is independent of the medium. For example, if 1 kg of two masses is kept in air or inside water, the gravitational force between the two masses remains the same. But the electrostatic force between the two charges depends on the nature of the medium in which the two charges are kept at rest.
7. Force Direction and Newton’s Third Law
The force on a charge q1 exerted by a point charge q2 is given by:
F12 = (1 / (4 π ε0)) (q1 q2 / r2) r̂21
Here, r̂21 is the unit vector from charge q2 to q1. But r̂12 = -r̂21, so:
F12 = -F21
Therefore, the electrostatic force obeys Newton’s third law.
8. Applicability of Coulomb’s Law
The expression for the Coulomb force is true only for point charges. Although a point charge is an ideal concept, we can apply Coulomb’s law to two charged objects whose sizes are much smaller than the distance between them. Coulomb discovered his law by considering charged spheres in a torsion balance as point charges. The distance between the two charged spheres was much greater than the radii of the spheres.