Current electricity class 12 notes: Ohm’s Law & V-I Characteristic Ohm’s Law & V-I Characteristics
Unit 2 • Current ElectricityUnderstanding the fundamental relationship between voltage, current, and resistance
Ohm’s Law
Definition:
At constant temperature and physical conditions, the current (I) through a conductor is directly proportional to the potential difference (V) across its ends.
Mathematical Form
Where:
V = Potential difference (Volts)
I = Current (Amperes)
R = Resistance (Ohms, Ω)
Experimental Verification
- Verified using voltmeter-ammeter method
- Slope of V-I graph gives resistance
- Valid only for ohmic conductors at constant temperature
- Materials that obey Ohm’s Law are called ohmic conductors
Limitations
- Only valid when physical conditions (especially temperature) remain constant
- Doesn’t apply to semiconductors, electrolytes, or gases
- Fails for devices like diodes, transistors, and thermistors
- Not valid for superconductors (where R=0)
V-I Characteristics
Ohmic Conductors
- Straight line passing through origin
- Constant slope (constant resistance)
- Examples: Metallic conductors (copper, aluminum)
- Follows Ohm’s Law precisely
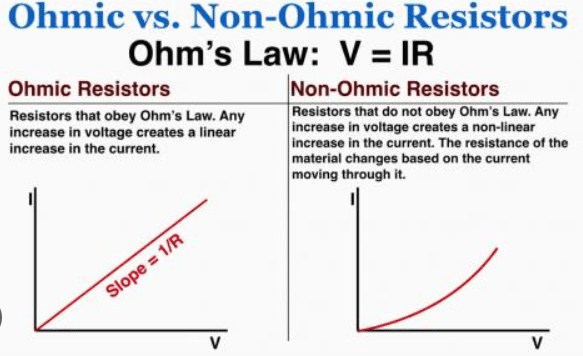
Non-Ohmic Conductors
- Non-linear relationship
- Slope changes (resistance varies with V or I)
- Examples: Diodes, transistors, thermistors
- Doesn’t obey Ohm’s Law

| Device | V-I Characteristic | Resistance Behavior |
|---|---|---|
| Copper wire | Linear | Constant |
| Semiconductor diode | Exponential | Decreases with voltage |
| Filament bulb | Curved | Increases with temperature |
| Thermistor | Non-linear | Decreases with temperature |
Resistance & Resistivity
Resistance (R)
Depends on:
- Material (resistivity ρ)
- Length (L) of conductor
- Cross-sectional area (A)
- Temperature
Resistivity (ρ)
Intrinsic property of material:
- Independent of dimensions
- Depends on temperature
- Metals: ρ increases with temperature
- Semiconductors: ρ decreases with temperature
Temperature Dependence
For conductors:
α = temperature coefficient of resistance (positive)
For semiconductors/thermistors:
β = material constant (negative temperature coefficient)
Worked Example
Problem:
A tungsten filament bulb has resistance of 240 Ω at 20°C. When operating at 2000°C, its resistance becomes 1200 Ω. Calculate:
- Temperature coefficient of resistance (α)
- Resistance at 1000°C
- Current at 2000°C when connected to 120V supply
Solution:
(1) Temperature coefficient (α):
(2) Resistance at 1000°C:
(3) Current at 2000°C:
Practice Problems
Problem 1
A 2m long copper wire (ρ = 1.68×10-8 Ω·m) has diameter 0.5mm. Calculate its resistance.
Problem 2
A semiconductor device has resistance 2kΩ at 20°C and 500Ω at 80°C. Calculate its temperature coefficient.
Problem 3
A diode has forward voltage drop of 0.7V at 10mA current. Calculate its dynamic resistance at this operating point.
Problem 4
An aluminum wire (α = 0.00429°C-1) has resistance 50Ω at 20°C. What temperature will increase its resistance by 20%?
Problem 5
A nichrome wire (ρ = 1.1×10-6 Ω·m) needs 10Ω resistance. If its diameter is 0.5mm, calculate required length.
Key Takeaways
Ohm’s Law Essentials
- V = IR is valid only for ohmic conductors
- Resistance depends on material and geometry
- Resistivity is intrinsic to the material
- Temperature affects resistance differently for metals vs semiconductors
Common Mistakes
- Assuming all materials obey Ohm’s Law
- Confusing static and dynamic resistance
- Forgetting temperature effects in calculations
- Using wrong temperature coefficient sign for semiconductors
Next Topic: Electrical Energy and Power
In the next section, we’ll explore how electrical energy is converted to other forms and calculate power dissipation in circuits.
Continue to Next Topic →