Exercise 11.2 Solutions (Class 9)
Surface Areas and Volumes
(Assume π = 22/7, unless stated otherwise)
1. Find the surface area of a sphere of radius:
Formula: Surface Area of a sphere = 4πr²
(i) 10.5 cm
Area = 4 × (22/7) × (10.5)² = 4 × (22/7) × 110.25 = 1386 cm².
(ii) 5.6 cm
Area = 4 × (22/7) × (5.6)² = 4 × (22/7) × 31.36 = 394.24 cm².
(iii) 14 cm
Area = 4 × (22/7) × 14² = 4 × 22 × 2 × 14 = 2464 cm².
2. Find the surface area of a sphere of diameter:
(i) 14 cm
Radius (r) = 14/2 = 7 cm.
Area = 4 × (22/7) × 7² = 4 × 22 × 7 = 616 cm².
(ii) 21 cm
Radius (r) = 21/2 = 10.5 cm.
Area = 4 × (22/7) × (10.5)² = 1386 cm².
(iii) 3.5 m
Radius (r) = 3.5/2 = 1.75 m.
Area = 4 × (22/7) × (1.75)² = 38.5 m².
3. Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Formula: Total Surface Area (TSA) of a hemisphere = 3πr².
Given: r = 10 cm.
TSA = 3 × 3.14 × 10² = 3 × 314 = 942 cm².
Answer: The total surface area of the hemisphere is 942 cm².
4. The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Let initial radius r₁ = 7 cm and final radius r₂ = 14 cm.
Initial Surface Area (S₁) = 4πr₁².
Final Surface Area (S₂) = 4πr₂².
Ratio S₁ / S₂ = (4πr₁²) / (4πr₂²) = r₁²/r₂² = (r₁/r₂)².
Ratio = (7/14)² = (1/2)² = 1/4.
Answer: The ratio of the surface areas is 1:4.
5. A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ₹16 per 100 cm².
Step 1: Find the inner radius and inner surface area.
Inner diameter = 10.5 cm, so inner radius (r) = 5.25 cm.
Inner surface area (CSA of hemisphere) = 2πr².
Area = 2 × (22/7) × (5.25)² = 173.25 cm².
Step 2: Calculate the cost of plating.
Cost per 100 cm² = ₹16. So, cost per 1 cm² = ₹16/100 = ₹0.16.
Total Cost = Area × Rate = 173.25 × 0.16 = ₹27.72.
Answer: The cost of tin-plating is ₹27.72.
6. Find the radius of a sphere whose surface area is 154 cm².
Given: Surface Area = 154 cm².
4πr² = 154
4 × (22/7) × r² = 154
r² = (154 × 7) / (4 × 22) = (7 × 7) / 4 = 49/4.
r = √(49/4) = 7/2 = 3.5 cm.
Answer: The radius of the sphere is 3.5 cm.
7. The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Let the diameter of the Earth be dE, and its radius be rE = dE/2.
Let the diameter of the Moon be dM, and its radius be rM = dM/2.
Given: dM = (1/4)dE. This implies rM = (1/4)rE.
Ratio of Surface Areas = (Surface Area of Moon) / (Surface Area of Earth)
= (4πrM²) / (4πrE²) = (rM/rE)².
Ratio = ((1/4)rE / rE)² = (1/4)² = 1/16.
Answer: The ratio of their surface areas is 1:16.
8. A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Step 1: Find the outer radius.
Inner radius (r) = 5 cm.
Thickness = 0.25 cm.
Outer radius (R) = Inner radius + Thickness = 5 + 0.25 = 5.25 cm.
Step 2: Calculate the outer curved surface area.
Outer CSA = 2πR² = 2 × (22/7) × (5.25)²
= 2 × (22/7) × 27.5625 = 173.25 cm².
Answer: The outer curved surface area is 173.25 cm².
9. A right circular cylinder just encloses a sphere of radius r (see Fig. 11.10). Find (i) surface area of the sphere, (ii) curved surface area of the cylinder, (iii) ratio of the areas obtained in (i) and (ii).
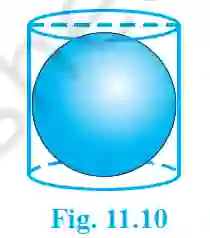 >
>Step 1: Determine the dimensions of the cylinder.
The radius of the cylinder’s base is the same as the sphere’s radius, r.
The height of the cylinder (h) is equal to the diameter of the sphere, so h = 2r.
(i) Surface area of the sphere:
Areasphere = 4πr².
(ii) Curved surface area of the cylinder:
CSAcylinder = 2πrh = 2πr(2r) = 4πr².
(iii) Ratio of the areas:
Ratio = (Areasphere) / (CSAcylinder) = (4πr²) / (4πr²) = 1/1.
Answer: The ratio is 1:1.


