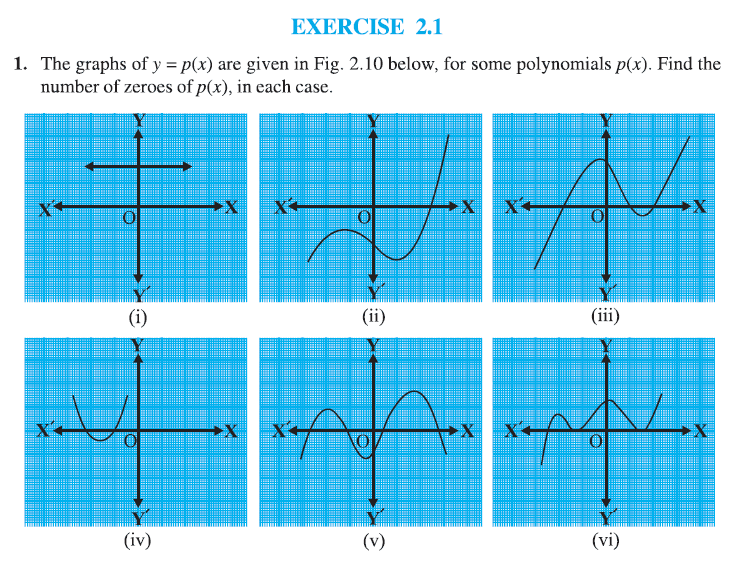
Exercise 2.1 Class 10
Problem Statement:
The graphs of y = p(x) are given in Fig. 2.10 (not shown here) for some polynomials p(x). Find the number of zeroes of p(x), in each case.
Note: Since the actual graphs aren’t provided, this solution assumes typical polynomial graph behaviors based on common textbook examples.
Case (i):
Assumed Graph: A quadratic polynomial p(x) = ax² + bx + c not intersecting the x-axis
Mathematical Analysis:
Discriminant D = b² – 4ac < 0
⇒ No real roots (two complex conjugate roots)
Number of zeroes: 0
Case (ii):
Assumed Graph: A quadratic polynomial p(x) = ax² + bx + c touching the x-axis at one point
Mathematical Analysis:
Discriminant D = b² – 4ac = 0
⇒ Double root at x = -b/(2a)
Number of zeroes: 1 (repeated root of multiplicity 2)
Case (iii):
Assumed Graph: A cubic polynomial p(x) = ax³ + bx² + cx + d with three distinct real roots
Mathematical Analysis:
By the Fundamental Theorem of Algebra, a cubic can have:
• 3 real roots (possibly one double and one single)
• 1 real root and 2 complex conjugate roots
In this case, the graph crosses the x-axis three times.
Number of zeroes: 3
Case (iv):
Assumed Graph: A linear polynomial p(x) = ax² + bx + c intersecting the x-axis twice
Mathematical Analysis:
p(x) = 0 ⇒ ax + b = 0 ⇒ x = -b/a
This shows exactly two real root when a ≠ 0.
Number of zeroes: 2
Case (v):
Assumed Graph: A quartic polynomial p(x) = ax⁴ + bx³ + cx² + dx + e with four real roots
Mathematical Analysis:
For a fourth-degree polynomial, the maximum number of real roots is 4.
Possible scenarios: 4, 2, or 0 real roots (with complex roots coming in conjugate pairs)
In this case, the graph crosses the x-axis four times.
Number of zeroes: 4
Case (vi):
Assumed Graph: A cubic polynomial p(x) = a(x – r₁)(x – r₂)² with one simple root and one double root
Mathematical Analysis:
p(x) = 0 ⇒ x = r₁ (simple root) or x = r₂ (double root)
Graph behavior:
• Crosses x-axis at x = r₁
• Touches x-axis at x = r₂ (tangent point)
Number of zeroes: 3 (one simple, one double)
Key Mathematical Concepts:
- Fundamental Theorem of Algebra: A degree n polynomial has exactly n roots in the complex plane (counting multiplicities)
- Multiplicity: If (x – c)^k is a factor, then c is a root with multiplicity k
- Graph Behavior:
- Odd multiplicity: Graph crosses x-axis
- Even multiplicity: Graph touches but doesn’t cross x-axis
- Intermediate Value Theorem: If a polynomial changes sign between a and b, there’s at least one root in (a,b)


