Exercise 7.3 Solutions (Class 9)
Triangles
1. ΔABC and ΔDBC are two isosceles triangles on the same base BC… Show that:
 >
>(i) ΔABD ≅ ΔACD:
In ΔABD and ΔACD:
• AB = AC (Given, ΔABC is isosceles)
• DB = DC (Given, ΔDBC is isosceles)
• AD = AD (Common side)
By SSS congruence rule, ΔABD ≅ ΔACD. (Proved)
(ii) ΔABP ≅ ΔACP:
In ΔABP and ΔACP:
• AB = AC (Given)
• ∠BAP = ∠CAP (From (i), by CPCT, since ΔABD ≅ ΔACD)
• AP = AP (Common side)
By SAS congruence rule, ΔABP ≅ ΔACP. (Proved)
(iii) AP bisects ∠A as well as ∠D:
From ΔABD ≅ ΔACD (part i), ∠BAP = ∠CAP, so AP bisects ∠A.
Also, ∠BDA = ∠CDA, so AP (or AD) bisects ∠D. (Proved)
(iv) AP is the perpendicular bisector of BC:
From ΔABP ≅ ΔACP (part ii), BP = CP (by CPCT), so AP bisects BC.
Also, ∠APB = ∠APC (by CPCT). Since ∠APB + ∠APC = 180° (linear pair), we have 2∠APB = 180°, so ∠APB = 90°.
Thus, AP is perpendicular to BC.
Since AP bisects BC and is perpendicular to it, AP is the perpendicular bisector of BC. (Proved)
2. AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that (i) AD bisects BC (ii) AD bisects ∠A.
Proof:
In right-angled triangles ΔADB and ΔADC:
• ∠ADB = ∠ADC = 90° (AD is an altitude)
• AB = AC (Given)
• AD = AD (Common side)
By RHS (Right-angle-Hypotenuse-Side) congruence rule, ΔADB ≅ ΔADC.
(i) AD bisects BC:
Since ΔADB ≅ ΔADC, their corresponding parts are equal. So, BD = CD (by CPCT). Thus, AD bisects BC. (Proved)
(ii) AD bisects ∠A:
Since ΔADB ≅ ΔADC, their corresponding angles are equal. So, ∠BAD = ∠CAD (by CPCT). Thus, AD bisects ∠A. (Proved)
3. Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR. Show that: (i) ΔABM ≅ ΔPQN (ii) ΔABC ≅ ΔPQR.
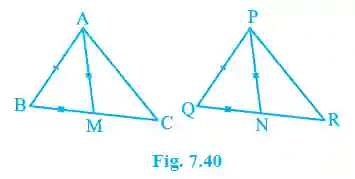 >
>(i) ΔABM ≅ ΔPQN:
Given: AM is median of ΔABC, so BM = 1/2 BC.
Given: PN is median of ΔPQR, so QN = 1/2 QR.
Since BC = QR, it follows that BM = QN.
In ΔABM and ΔPQN:
• AB = PQ (Given)
• BM = QN (Proved above)
• AM = PN (Given)
By SSS congruence rule, ΔABM ≅ ΔPQN. (Proved)
(ii) ΔABC ≅ ΔPQR:
Since ΔABM ≅ ΔPQN, we have ∠B = ∠Q (by CPCT).
Now, in ΔABC and ΔPQR:
• AB = PQ (Given)
• ∠B = ∠Q (Proved above)
• BC = QR (Given)
By SAS congruence rule, ΔABC ≅ ΔPQR. (Proved)
4. BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Proof:
Consider the right-angled triangles ΔBFC and ΔCEB.
• ∠BFC = ∠CEB = 90° (Given altitudes)
• BC = CB (Common hypotenuse)
• CF = BE (Given equal altitudes)
By RHS congruence rule, ΔBFC ≅ ΔCEB.
Since the triangles are congruent, their corresponding angles are equal.
So, ∠FBC = ∠ECB (by CPCT).
This means ∠ABC = ∠ACB.
In ΔABC, sides opposite to equal angles are equal.
Therefore, AC = AB. This means ΔABC is an isosceles triangle. (Proved)
5. ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that ∠B = ∠C.
Construction: Draw altitude AP from A to BC.
Proof:
In right-angled triangles ΔAPB and ΔAPC:
• ∠APB = ∠APC = 90° (By construction)
• AB = AC (Given)
• AP = AP (Common side)
By RHS congruence rule, ΔAPB ≅ ΔAPC.
Since the triangles are congruent, their corresponding angles are equal.
Therefore, ∠B = ∠C (by CPCT).
(Proved)