Exercise 8.2 Solutions (Class 9)
Quadrilaterals
1. ABCD is a quadrilateral in which P, Q, R and S are mid-points of the sides AB, BC, CD and DA. AC is a diagonal. Show that: (i) SR || AC and SR = 1/2 AC (ii) PQ = SR (iii) PQRS is a parallelogram.
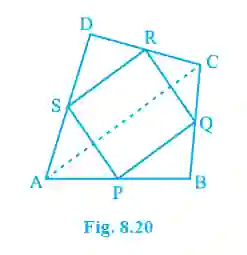 >
>(i) Show SR || AC and SR = 1/2 AC:
In ΔDAC, S is the mid-point of DA and R is the mid-point of DC.
By the Mid-point Theorem, the line segment joining the mid-points of two sides of a triangle is parallel to the third side and half of it.
Therefore, SR || AC and SR = (1/2)AC. (Proved)
(ii) Show PQ = SR:
In ΔBAC, P is the mid-point of AB and Q is the mid-point of BC.
By the Mid-point Theorem, PQ || AC and PQ = (1/2)AC.
From part (i), we have SR = (1/2)AC. Therefore, PQ = SR. (Proved)
(iii) Show PQRS is a parallelogram:
From the proofs above, we have PQ || AC and SR || AC, which implies PQ || SR.
We also have PQ = SR.
Since one pair of opposite sides (PQ and SR) is both equal and parallel, the quadrilateral PQRS is a parallelogram. (Proved)
2. ABCD is a rhombus and P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rectangle.
Join diagonals AC and BD. From Q1, we know PQRS is a parallelogram.
In ΔADC, SR || AC and SR = 1/2 AC.
In ΔABC, PQ || AC and PQ = 1/2 AC.
In ΔADB, SP || BD and SP = 1/2 BD.
In ΔCDB, RQ || BD and RQ = 1/2 BD.
The diagonals of a rhombus (AC and BD) bisect each other at right angles. So, AC ⊥ BD.
Since SR || AC and RQ || BD, the angle between SR and RQ must be the same as the angle between AC and BD.
Therefore, SR ⊥ RQ, which means ∠SRQ = 90°.
A parallelogram with one right angle is a rectangle. Hence, PQRS is a rectangle. (Proved)
3. ABCD is a rectangle and P, Q, R and S are mid-points of the sides AB, BC, CD and DA respectively. Show that the quadrilateral PQRS is a rhombus.
Join diagonals AC and BD. From Q1, we know PQRS is a parallelogram.
In ΔABC, by Mid-point Theorem, PQ = 1/2 AC.
In ΔADC, by Mid-point Theorem, SR = 1/2 AC. So PQ = SR.
In ΔABD, by Mid-point Theorem, SP = 1/2 BD.
In ΔBCD, by Mid-point Theorem, RQ = 1/2 BD. So SP = RQ.
The diagonals of a rectangle are equal, so AC = BD.
Therefore, PQ = SP = RQ = SR (since each is half of the equal diagonals).
A parallelogram with all four sides equal is a rhombus. Hence, PQRS is a rhombus. (Proved)
4. ABCD is a trapezium in which AB || DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F. Show that F is the mid-point of BC.
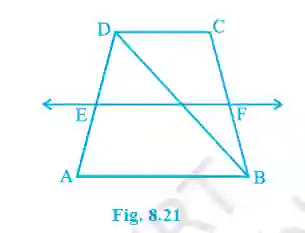 >
>Given: Trapezium ABCD, AB || DC. E is mid-point of AD. EF || AB.
To Prove: F is the mid-point of BC.
Construction: Let EF intersect diagonal BD at G.
Proof:
In ΔDAB, E is the mid-point of AD and EG || AB (since EF || AB).
By the Converse of the Mid-point Theorem, a line drawn through the mid-point of one side of a triangle, parallel to another side, bisects the third side.
Therefore, G is the mid-point of DB.
Now, in ΔBCD, G is the mid-point of DB (proved above).
Also, since AB || DC and EF || AB, it follows that EF || DC. So, GF || DC.
Again, by the Converse of the Mid-point Theorem, F must be the mid-point of BC.
(Proved)
5. In a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.
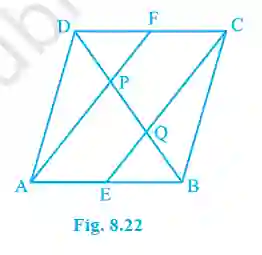 >
>Since ABCD is a parallelogram, AB || CD and AB = CD.
This means AE || FC and AE = 1/2 AB = 1/2 CD = FC.
Since one pair of opposite sides (AE and FC) is equal and parallel, AECF is a parallelogram. Therefore, AF || EC.
In ΔDQC, F is the mid-point of DC and FP || CQ (since AF || EC). By Converse of Mid-point theorem, P is the mid-point of DQ. So, DP = PQ. —(1)
In ΔAPB, E is the mid-point of AB and EQ || AP (since AF || EC). By Converse of Mid-point theorem, Q is the mid-point of PB. So, PQ = QB. —(2)
From (1) and (2), we have DP = PQ = QB. This means the segments AF and EC divide the diagonal BD into three equal parts.
(Proved)
6. ABC is a triangle right angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that (i) D is the mid-point of AC (ii) MD ⊥ AC (iii) CM = MA = 1/2 AB.
(i) D is the mid-point of AC:
In ΔABC, M is the mid-point of AB and MD || BC. By the Converse of the Mid-point Theorem, D must be the mid-point of the third side AC. (Proved)
(ii) MD ⊥ AC:
Given MD || BC. Since BC ⊥ AC (∠C = 90°), the corresponding angles are equal.
Therefore, ∠MDC = ∠BCA = 90°. This means MD ⊥ AC. (Proved)
(iii) CM = MA = 1/2 AB:
Join CM. In ΔADM and ΔCDM:
• AD = CD (D is the mid-point)
• ∠ADM = ∠CDM = 90° (Proved)
• MD = MD (Common)
By SAS congruence, ΔADM ≅ ΔCDM. So, CM = AM (by CPCT).
Since M is the mid-point of AB, AM = 1/2 AB.
Therefore, CM = AM = 1/2 AB. (Proved)