Understanding the Refraction of Light
Introduction
Refraction of Light is a fascinating phenomenon that occurs when light waves change direction as they pass from one medium to another. This bending of light is responsible for many everyday visual effects and has significant applications in fields like optics and astronomy. In this blog post, we’ll delve into the principles, causes, examples, and applications of light refraction.
What is Refraction?
Refraction is the bending of light as it passes from one transparent medium to another with a different density. This change in direction is due to the change in speed of light in different media. For instance, light travels slower in water than in air, causing it to bend towards the normal when entering the water.
The Laws of Refraction
First Law of Refraction: The incident ray, the refracted ray, and the normal to the interface of two media all lie in the same plane.
Second Law of Refraction (Snell’s Law): This law provides the relationship between the angles of incidence and refraction, given by the equation:
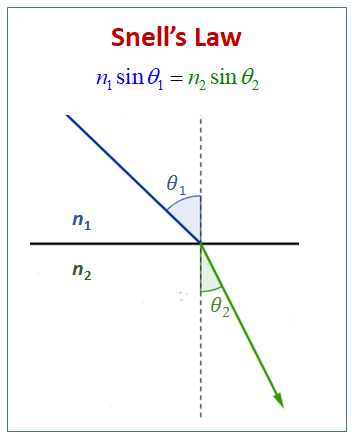 >
>Refractive Index
The refractive index is a measure of how much light bends when it enters a medium. It is defined as the ratio of the speed of light in a vacuum to the speed of light in the medium. A higher refractive index indicates that light slows down more and bends more when entering the medium.
Numericals
Refractive Index Problems
1. The speed of light in a vacuum is \(3 \times 10^8\) m/s. If the speed of light in a medium is \(2 \times 10^8\) m/s, what is the refractive index of the medium?
The refractive index \(n\) is given by the formula \(n = \frac{c}{v}\), where \(c\) is the speed of light in a vacuum and \(v\) is the speed of light in the medium. So, \(n = \frac{3 \times 10^8}{2 \times 10^8} = 1.5\).
2. A ray of light passes from air into water with a refractive index of 1.33. If the angle of incidence in the air is 30°, what is the angle of refraction in the water?
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1\), \(n_2 = 1.33\), \(\theta_1 = 30^\circ\). So, \(\sin \theta_2 = \frac{\sin 30^\circ}{1.33} = \frac{0.5}{1.33} \approx 0.376\). Therefore, \(\theta_2 \approx \arcsin(0.376) \approx 22.09^\circ\).
3. Calculate the critical angle for total internal reflection at the boundary between water (n = 1.33) and air (n = 1).
The critical angle \(\theta_c\) is given by \(\sin \theta_c = \frac{n_2}{n_1}\). Here, \(n_1 = 1.33\) (water), \(n_2 = 1\) (air). So, \(\sin \theta_c = \frac{1}{1.33} \approx 0.752\). Therefore, \(\theta_c \approx \arcsin(0.752) \approx 48.75^\circ\).
4. If a light ray passes from glass (n = 1.5) to water (n = 1.33) with an angle of incidence of 45°, what is the angle of refraction in the water?
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1.5\), \(n_2 = 1.33\), \(\theta_1 = 45^\circ\). So, \(\sin \theta_2 = \frac{1.5 \sin 45^\circ}{1.33} = \frac{1.5 \times 0.707}{1.33} \approx 0.797\). Therefore, \(\theta_2 \approx \arcsin(0.797) \approx 52.25^\circ\).
5. The refractive index of diamond is 2.42. What is the speed of light in diamond?
The speed of light \(v\) in a medium is given by \(v = \frac{c}{n}\), where \(c\) is the speed of light in vacuum and \(n\) is the refractive index. So, \(v = \frac{3 \times 10^8}{2.42} \approx 1.24 \times 10^8\) m/s.
6. A light ray enters a rectangular glass slab (n = 1.5) at an angle of 30°. What is the angle of refraction inside the glass slab?
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1\) (air), \(n_2 = 1.5\), \(\theta_1 = 30^\circ\). So, \(\sin \theta_2 = \frac{\sin 30^\circ}{1.5} = \frac{0.5}{1.5} \approx 0.333\). Therefore, \(\theta_2 \approx \arcsin(0.333) \approx 19.47^\circ\).
7. A light ray travels from water (n = 1.33) into glass (n = 1.5). If the angle of incidence in water is 40°, what is the angle of refraction in glass?
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1.33\), \(n_2 = 1.5\), \(\theta_1 = 40^\circ\). So, \(\sin \theta_2 = \frac{1.33 \sin 40^\circ}{1.5} = \frac{1.33 \times 0.643}{1.5} \approx 0.570\). Therefore, \(\theta_2 \approx \arcsin(0.570) \approx 34.80^\circ\).
8. Calculate the refractive index of a medium if the angle of incidence in air is 60° and the angle of refraction in the medium is 30°.
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1\) (air), \(\theta_1 = 60^\circ\), \(\theta_2 = 30^\circ\). So, \(n_2 = \frac{\sin 60^\circ}{\sin 30^\circ} = \frac{0.866}{0.5} = 1.732\).
9. A light ray passes from a medium with refractive index 1.2 into a medium with refractive index 1.6. If the angle of incidence is 35°, what is the angle of refraction?
Using Snell’s Law: \(n_1 \sin \theta_1 = n_2 \sin \theta_2\). Here, \(n_1 = 1.2\), \(n_2 = 1.6\), \(\theta_1 = 35^\circ\). So, \(\sin \theta_2 = \frac{1.2 \sin 35^\circ}{1.6} = \frac{1.2 \times 0.574}{1.6} \approx 0.4305\). Therefore, \(\theta_2 \approx \arcsin(0.4305) \approx 25.48^\circ\).
10. Determine the refractive index of a medium if the speed of light in the medium is \(2.25 \times 10^8\) m/s.
The refractive index \(n\) is given by \(n = \frac{c}{v}\), where \(c\) is the speed of light in a vacuum and \(v\) is the speed of light in the medium. So, \(n = \frac{3 \times 10^8}{2.25 \times 10^8} \approx 1.33\).
Factors Affecting Refraction
Several factors influence the degree of refraction:
- Wavelength: Different wavelengths of light refract by different amounts. This is why prisms can separate white light into its constituent colors, creating a spectrum.
- Medium Density: The optical density of the medium affects the speed of light and, consequently, the angle of refraction.
- Angle of Incidence: The initial angle at which light hits the boundary between two media also affects the degree of bending.
Common Examples of Refraction
Refraction manifests itself in various everyday phenomena:
- Bending of a Straw in Water: A straw appears bent when submerged in water due to the refraction of light at the water-air interface.
- Mirages: Created by the refraction of light in layers of air at different temperatures, leading to the illusion of water on roads.
- Lenses: Convex and concave lenses use refraction to focus or diverge light, forming images.
Applications of Refraction
Refraction has numerous practical applications, including:
- Eyeglasses and Contact Lenses: Correct vision by refracting light to focus it properly on the retina.
- Cameras: Use lenses to focus light and capture clear images.
- Microscopes and Telescopes: Magnify small or distant objects by refracting light through multiple lenses.
- Optical Fibers: Transmit light signals over long distances by continually refracting light within the fiber.
Experiments Demonstrating Refraction
Engaging in simple experiments can help visualize refraction:
- Glass of Water and Pencil: Place a pencil in a glass of water and observe the apparent bending.
- Prism and White Light: Shine a beam of white light through a glass prism to observe the dispersion into a spectrum.
- Laser Pointer and Different Media: Shine a laser through different transparent materials to see how the light path changes.
Conclusion
Refraction is a fundamental concept in optics, with significant implications in everyday life and various technological applications. By understanding the principles and effects of refraction, we can better appreciate the interactions of light with different media and harness these properties in innovative ways.


