The Complete Guide to Refractive Index: Concept, Types, and Examples
1. What is Refractive Index?
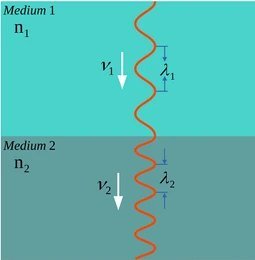
The refractive index, denoted as n, describes how light changes direction, or refracts, when it enters a different medium. It quantifies the extent to which light slows down as it travels from one medium to another.
2. Expression and Formula for Refractive Index
The refractive index n can be mathematically expressed as:
n = c / v
Where:
- n = refractive index
- c = speed of light in vacuum (≈ 3 × 108 m/s)
- v = speed of light in the medium
3. Types of Refractive Indices
- Absolute Refractive Index: Ratio of the speed of light in a vacuum to that in a medium.
- Relative Refractive Index: Ratio of light speed between two media.
- Complex Refractive Index: Accounts for both refraction and absorption.
4. Examples of Refractive Indices of Common Materials
| Medium | Refractive Index (Approximate) |
|---|---|
| Vacuum | 1 |
| Air (at STP) | 1.0003 |
| Water | 1.33 |
| Glass | 1.5 |
| Diamond | 2.42 |
5. Practice Numericals on Refractive Index
Numerical 1: Calculate the refractive index of a medium in which the speed of light is 2 × 108 m/s.
Solution:
n = c / v = 3 × 108 / 2 × 108 = 1.5
Numerical 2: If the refractive index of water is 1.33, what is the speed of light in water?
Solution:
v = c / n = 3 × 108 / 1.33 ≈ 2.26 × 108 m/s
Numerical 3: Light passes from air (n = 1) to glass (n = 1.5). If the angle of incidence is 30°, find the angle of refraction.
Solution:
sin θ2 = (n1 / n2) sin θ1 = (1 / 1.5) sin 30°
sin θ2 = 0.333
θ2 ≈ 19.47°
Numerical 4: A beam of light in air strikes a medium with a refractive index of 2 at an angle of 45°. Find the angle of refraction.
Solution:
sin θ2 = sin 45° / 2 = 0.3536
θ2 ≈ 20.7°
Numerical 5: The refractive index of ethanol is 1.36. Calculate the speed of light in ethanol.
Solution:
v = c / n = 3 × 108 / 1.36 ≈ 2.21 × 108 m/s
Numerical 6: A light ray passes from medium A to medium B. If the refractive indices are 1.5 and 1.2 respectively, and the angle of incidence is 50°, find the angle of refraction.
Solution:
sin θ2 = (1.5 / 1.2) sin 50° ≈ 75.2°
Numerical 7: If the refractive index of a material is 2.4, and light enters at 45°, find the angle of refraction.
Solution:
sin θ2 = sin 45° / 2.4 = 0.294
θ2 ≈ 17.1°
Numerical 8: A material has a refractive index of 1.8. What would be the speed of light in this material?
Solution:
v = c / n = 3 × 108 / 1.8 ≈ 1.67 × 108 m/s
Numerical 9: For a refractive index of 1.6 and a light incident angle of 60°, find the angle of refraction.
Solution:
sin θ2 = sin 60° / 1.6 ≈ 32.6°
Numerical 10: If the refractive index between two media is 1.33 and the angle of incidence is 30°, find the angle of refraction.
Solution:
sin θ2 = sin 30° / 1.33 ≈ 22°