Important Points Of Crystal lattice and Unit Cell Class12

Introduction of Crystal lattice and Unit Cell

The component particles of Crystal lattice and Unit Cell are precisely arranged in three dimensions. Points are often used to represent the relative positions of these particles inside a crystal. The phrase “space lattice” refers to the configuration of an infinite set of these points. Lattice points, also known as lattice sites, are the locations in the crystal lattice that are occupied by atoms, ions, or molecules.

Crystal lattice and Unit Cell

Understanding Two-Dimensional Lattices

A two-dimensional lattice is a regular, repeating arrangement of atoms, ions, or molecules in a plane. These arrangements form specific patterns, leading to five fundamental types of two-dimensional lattices, each with distinct symmetry properties.

Types of Two-Dimensional Lattices

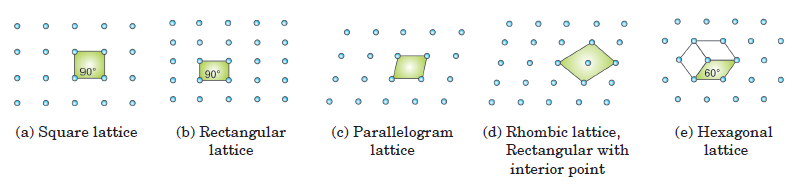
1. Square Lattice:
   • Symmetry: The square lattice has high symmetry due to equal side lengths and 90° angles between adjacent edges. This arrangement allows the lattice to appear identical when rotated by 90°, 180°, or 270°.
   • Unit Cell: The simplest unit cell for a square lattice is a square, where each side has the same length. This symmetry results in uniform spacing and a repeating square pattern.
   • Applications: Square lattices are found in simple cubic crystal structures, certain metals, and minerals. They provide a foundation for understanding more complex crystal arrangements.
2. Rectangular Lattice:
   • Symmetry: A rectangular lattice has sides of different lengths but maintains 90° angles. This asymmetry means the lattice looks the same only when rotated by 180°.
   • Unit Cell: The unit cell is a rectangle, where the length and width are distinct. Despite having two axes of different lengths, the angles remain consistent at 90°.
   • Applications: Rectangular lattices are used to model orthorhombic crystal systems and can be observed in certain polymers and layered materials.
3. Parallelogram Lattice:
   • Symmetry: This lattice has the least symmetry, with unequal sides and non-right angles. The arrangement of points forms a repeating parallelogram, and the lattice does not have consistent rotational symmetry.
   • Unit Cell: The unit cell is a parallelogram, characterized by its four sides and the angles between them, which are not 90°.
   • Applications: Parallelogram lattices are used to describe the structure of some molecular crystals and are essential in studying materials with low symmetry.
4. Rhombic Lattice:
   • Symmetry: The rhombic lattice consists of equal-length sides but with angles that are not 90°. It can be seen as a stretched or skewed square, retaining a consistent side length but variable internal angles.
   • Unit Cell: The standard representation of the unit cell is a rhombus, where all sides are equal but angles are typically 60° or 120°. Alternatively, a rectangular unit cell with an inner point (centered unit cell) can be used.
   • Applications: Rhombic lattices appear in certain crystal structures like monoclinic systems and in some organic compounds.
5. Hexagonal Lattice:
   • Symmetry: The hexagonal lattice has the highest symmetry among the two-dimensional lattices. It features equal side lengths and internal angles of 120°, resulting in a repeating hexagonal pattern.
   • Unit Cell: The unit cell is a rhombus with a 60° angle or equivalently, a hexagon divided into rhombic sections. This symmetry allows for complex tiling and efficient packing.
   • Applications: Hexagonal lattices are prominent in graphene, boron nitride, and certain metals. They are crucial in materials science for understanding high-symmetry crystal systems.

Unit Cells and Their Importance

A unit cell is the smallest portion of a lattice that can be used to recreate the entire structure through translation. Understanding unit cells is key to visualizing and characterizing the overall lattice.

• Primitive Unit Cell: A simple cell that contains only one lattice point at each corner. It is the smallest and most fundamental representation of the lattice.
• Centred Unit Cell: Contains additional points within the cell, such as a point at the centre or other symmetric positions. This is useful for describing more complex lattices, such as those with additional symmetry or multiple atomic species.

Characteristics of Unit Cells

The characteristics of the unit cell—such as the lengths of the edges and the angles between them—are fundamental in defining the lattice. These parameters determine how the unit cell can be translated to cover the entire lattice.

• Edge Lengths: The length of the edges determines the spacing between repeating points in the lattice.
• Angles: The angles between the edges define the shape of the unit cell and influence the symmetry of the lattice.

B. Three-Dimensional Crystal Lattice

Crystal lattice (space lattice)

• Definition: A crystal lattice is a three-dimensional framework or grid where each point represents the position of a constituent particle in a crystalline solid.
• Visualization: Imagine a vast grid of points, extending infinitely in all directions. Each point on this grid represents a particle’s specific position in the solid.
• Importance:
  • It helps to understand the symmetrical arrangement of particles in a crystal.
  • Determines the physical properties of the crystalline material.
• Analogy: Think of a crystal lattice like a 3D chessboard, where each point (intersection) represents a location for a piece (particle).

Characteristics of a Crystal Lattice

1. Lattice Point or Lattice Site:

Each point in a crystal lattice where a particle (atom, ion, or molecule) is located.

1. Three-Dimensional Arrangement:

The orderly, repeating arrangement of lattice points forms the structure of the crystal.

2. Geometry:

The overall shape and symmetry of the lattice can be visualized by connecting the lattice points with lines.

2. Example: Picture connecting dots on graph paper to reveal a pattern or shape.

Unit Cell: The Fundamental Building Block

• Definition: The unit cell is the smallest portion of a crystal lattice that repeats in space to form the entire lattice.
• Importance:
  • It defines the geometric structure of the crystal.
  • Knowing the unit cell allows us to understand and calculate various properties of the crystal, such as density and packing efficiency.
• Analogy: Imagine a single tile on a patterned floor. When you repeat this tile over and over, you get the entire floor design.

Properties of a Unit Cell

1. Dimensions (edge lengths):
   • Edges are denoted by a, b, and c.
   • Description: These are the lengths of the unit cell’s sides.
   • Analogy: Think of the dimensions like the sides of a small box.
2. Angles:
   • α (Alpha): Angle between edges b and c.
   • β (Beta): Angle between edges c and a.
   • γ (Gamma): Angle between edges a and b.
   • Analogy: Imagine tilting the corners of a box so that they meet at these specific angles.

Summary: The unit cell is characterized by three edge lengths (a, b, c) and three angles (α, β, γ). The complete crystal lattice is built by repeating the unit cell in three dimensions.

Types of Unit Cells

1. Primitive (simple) Unit Cells

• Definition: unit cells in which particles are only at the corners.
• Characteristics:
  • The simplest form of unit cell.
  • Each corner particle is shared among eight adjacent unit cells.
  • Number of Particles: contains one complete particle per unit cell.
• Analogy: Like a cube with marbles placed only at the corners.

2. Non-Primitive (Centered) Unit Cells

• Definition: unit cells with particles at the corners and additional positions within the cell.
• Characteristics:
  • More complex than primitive cells, offering better packing and often higher symmetry.
• Types:
  • Face-Centered Cubic (FCC):
    • Particles are located in the corners and centers of each face.
    • Example: Like a cube with marbles at each corner and in the middle of each face.
    • Number of Particles: contains four particles per unit cell.
    • Found in metals like aluminium and copper.
  • Body-centred Cubic (BCC):
    • Particles are in the corners and centre of the unit cell.
    • Example: Like a cube with marbles at each corner and one in the centre.
    • Number of Particles: contains two particles per unit cell.
    • Found in: metals like iron.
  • End-centered Unit Cells:
    • Particles are at the corners and centres of two opposite faces.
    • Example: Like a cube with marbles at the corners and in the middle of two opposing faces.
    • Number of Particles: contains two particles per unit cell.
    • Found in certain minerals and ceramics.

Seven Crystal Systems

1. Cubic System

• Characteristics:
  • All sides ((a = b = c) are of equal length.
  • All angles are 90°.
• Unit Cells: Simple cubic, BCC, FCC.
• For example, consider perfectly shaped dice.
• Found in: salt crystals (NaCl), diamonds.

2. Tetragonal System

• Characteristics:
  • Two sides are equal; the third is different (a = b ≠ c,).
  • All angles are 90°.
• Unit Cells: Simple, BCC.
• Example: Like stretched dice.
• Found in: white tin, certain minerals.

3. Orthorhombic System

• Characteristics:
  • All sides are of different lengths (a ≠ b ≠ c,).
  • All angles are 90°.
• Unit Cells: Simple, BCC, FCC, end-centered.
• Example: Like a shoebox with different dimensions.
• Found in: sulfur, topaz.

4. Monoclinic System

• Characteristics:
  • All sides are of different lengths a ≠ b ≠ c).
  • Two angles are 90°; the third is not.
• Unit Cells: Simple, end-centered.
• For example, consider a leaning shoebox.
• Found in: gypsum, sugar.

5. Hexagonal System

• Characteristics:
  • Two sides are equal (a = b ≠ c,).
  • Two angles are 90°; one is 120°.
• Unit Cells: Simple.
• For example, consider a hexagonal pencil.
• Quartz and graphite are found.

6. The Rhombohedral (Trigonal) System

• Characteristics:
  • All sides are equal (a = b = c).
  • All angles are equal, but not 90°.
• Unit Cells: Simple.
• An example is a squished cube.
• Calcite and cinnabar are found.

7. Triclinic System

• Characteristics:
  • All sides are of different lengths (a ≠ b ≠ c,).
  • All angles are different, and none are 90°.
• Unit Cells: Simple.
• For example, consider a distorted box with no right angles.
• Kyanite and turquoise are found.

Note: Each crystal system can have different types of lattices, leading to diverse structures and properties.

Types of Cubic Lattices

1. Simple (Primitive) Cubic

• Characteristics:
  • Particles only at the corners.
  • Number of Particles : contains one particle per unit cell.
• Visualization: Like a cube with marbles at each corner.
• Polonium (Po), for example.

2. Body-Centered Cubic (BCC)

• Characteristics:
  • Particles at the corners and the center.
  • Number of Particles: contains two particles per unit cell.
• Visualization: A cube with marbles at each corner and one in the center.
• Example: iron (Fe), tungsten (W).

3. Face-Centered Cubic (FCC)

• Characteristics:
  • Particles at the corners and the centers of each face.
  • Number of Particles: contains four particles per unit cell.
• Visualization: A cube with marbles at each corner and in the middle of each face.
• Example: aluminum (Al), copper (Cu).

Overall, crystalline structures are defined by the symmetry and arrangement of their constituent particles. Understanding the types of unit cells and crystal systems aids in predicting and explaining materials’ physical properties.